 |
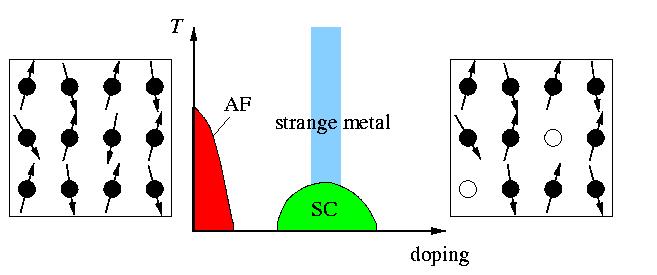
Schematic phase diagram.
AF = antiferromagnet
|
 Structure of YBa2Cu3O7 .
(Courtesy of Frank Hewat, ILL)
Structure of YBa2Cu3O7 .
(Courtesy of Frank Hewat, ILL)
These systems consist of strongly correlated electrons moving in CuO planes. At half-filling, there is exactly one electron per unit cell. There is strong Coulomb repulsion between the electrons. This leads to an electronic traffic jam -- the ground state is an insulator. Exchange effects mean that electrons on neighboring sites prefer to have antiparallel spins, and so this insulator is antiferromagnet. This is depicted on the diagram below on the left hand side.
The traffic jam can be relieved by removing electrons from the CuO planes. This is done by chemical doping. We now have a metal that conducts electricity. The mobile carriers are the vacancies (holes) moving in an antiferromagnetic background. Further doping eventually destroys the antiferromagnetic order, and one finds a range of doping where the system is a superconductor below a transition temperature Tc of the order of 100K.
 |
Schematic phase diagram.
AF = antiferromagnet
|
We have investigated a model of degenerate bosons in a random quasistatic magnetic field, motivated by the idea of spin-charge separation. In the slave-boson treatment of the t-J model, a physical hole is represented by a charged boson ("holon") and a neutral spin-half fermion ("spinon") which interact via an internal gauge field. To study charge properties, we have focused on the dynamics of the charged bosons only. The random field destroys superfluidity at all finite temperatures, giving rise to a metallic phase of degenerate bosons. A quantum Monte Carlo study has successfully demonstrated that the resistivity of this Bose metal is indeed linear in temperature with a scattering rate of 2kT, irrespective of density.
Open questions remain about the anomalous Hall effect. In these systems, the Hall coefficient is close to 1/nec near the superconducting transition (n is the number of doped holes), but decreases away from this classical value as 1/T with increasing temperature! This is surprising because this seems to imply that a scattering rate proportional to T2, contradicting the resistivity data (see above). We propose that the Hall data probes a new scattering rate: the decay rate of the physical hole into a holon and a spinon in our picture of spin-charge separation.