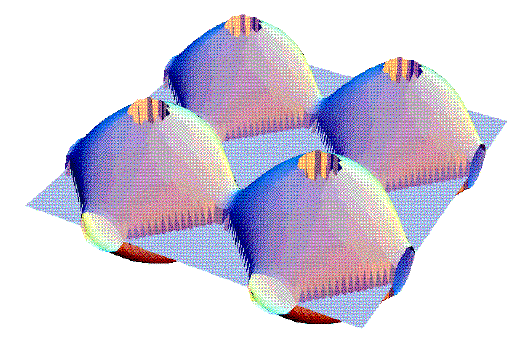Photonic Dispersion Surfaces
The figure below shows a dispersion surface for the logpile system. This is produced by finding all the allowed k-vectors at a fixed frequency. The tips of these vectors describe a surface of constant energy in k-space - the so called dispersion surface. The Fermi surface for electrons in a metal is a more familar example of this idea. Of course for photons there are two surfaces, one for each polarisation. For clarity we show only the dispersion surface for a single polarisation.
The surface is shown in an extended zone scheme. Notice the large holes -
regions for which there are no allowed states in k-space. These
correspond to directions in real space in which propagation is forbidden. By
focusing attention on the dispersion surface we hope to find ways of
eliminating what remains of the surface, thus pushing the system into the
insulating regime where propagation is forbidden in all directions.