Maxwell and Geometry


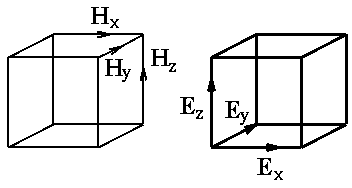
Maxwell's equations,
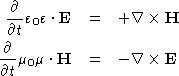
eqnarray3
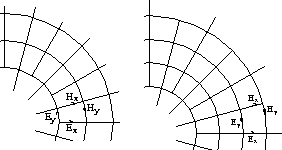
can be represented geometrically. Define two simple cubic lattices - unit cells shown on the left. Along the edges of one arrange the E fields, along the edges of the other, the H fields.

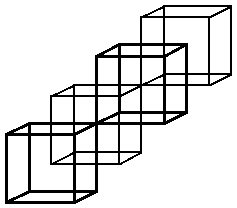
Next arrange the two lattices so that they interpenetrate: one lattice centres the other. Note that each face of the H lattice is pierced by a line of force of the E lattice. Applying Stokes theorem around the edges of the face gives the first Maxwell equation. Similarly the second equation can be obtained by considering faces of the E lattice. Even if the lattice is distorted, we can still apply Stokes and get some equations.

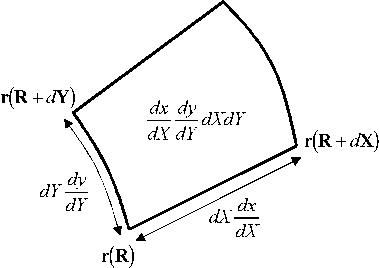
These can be transformed back to the original Maxwell's equations on the undistorted lattice provided that we modify tex2html_wrap_inline32 and tex2html_wrap_inline34 and the fields.
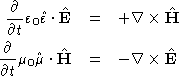
eqnarray13



All the geometry is subsumed in tex2html_wrap_inline32 and tex2html_wrap_inline34. Thus we need only write our computer codes in one coordinate frame. All other topologically equivalent frames can be accommodated by adjusting tex2html_wrap_inline32 and tex2html_wrap_inline34.



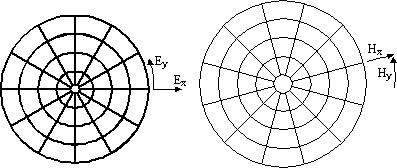
For example we can work with a cylindrical coordinate system to treat fibres and wires: