Maximal Fluctuations

Theorem

Waves incident on disordered systems are partly reflected and partly transmitted - think of light incident on snow. White light penetrates snow as a uniform diffuse glow, but if instead of white light we use a laser of fixed frequency, the uniform glow breaks up into intensely bright regions separated by dark spots - a speckle pattern. We have been able to characterise these fluctuations by a very general theorem: let the amplitude transmission coefficient for transmission from point r' to point r be T_rr' . Then,

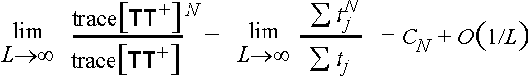
The Theorem Interpreted

The eigenvectors of TT⁺ define a set of channels through which light can be transmitted. The eigenvalues of TT⁺, t_j, define the corresponding transmission coefficients and it is with the eigenvalues that the theorem is exclusively concerned. Imagine what would happen if C_N were exactly unity. Then the t_j would have to be either 1 or 0 so that raising to the Nth power has no effect. In practice the C_N are not exactly unity, but they are of that order. So our result is that transmission in the individual channels is either of order unity, or essentially insignificant.

Even in a very thick sample through which little light penetrates on average, there will be some occasions when the light shines through brightly. Surprised?

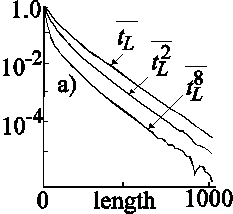
An example in 1D

a) Moments of the transmission coefficient, t_L , of 1D samples, length L, calculated by averaging over 9,259,648 samples.
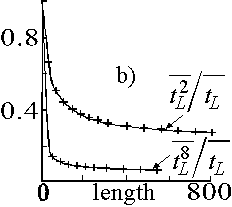
b) Ratios of the moments of t_L Theoretical predictions are denoted by '+' symbols.