Types of Equations

The PDE's which occur in physics are mostly second order^2.1. The work in this section is also considered in chapter III of Potter (1973) and chapter 17 of Press et al. (1992). For linear equations in 2 dimensions there is a simple classification in terms of the general equation

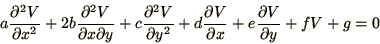$$a{\partial^2 V\over\partial x^2} +2 b {\partial^2 V\over\p... ...er\partial x} + e {\partial V\over\partial y} + f V + g = 0$$ (2.1)

as shown in the following table

Condition	Type	Example
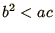$b^2 < ac$	Elliptic	Laplace's equation (2.2)
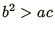$b^2 > ac$	Hyperbolic	Wave equation (2.3)
$b^2 = ac$	Parabolic	Diffusion/Schrödinger equation (2.4)

These are listed in their simplest form as follows (with the substitution 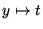$y\mapsto t$ where appropriate)

$$\mbox{Laplace's equation}\qquad {\partial^2 V\over\partial x^2} + {\partial^2 V\over\partial y^2} = 0$$ (2.2)

$$\mbox{Wave equation}\qquad {\partial^2 V\over\partial x^2} - {1\over c^2}{\partial^2 V\over\partial t^2} = 0$$ (2.3)

$$\mbox{Diffusion equation}\qquad D{\partial^2 V\over\partial x^2} - {\partial V\over\partial t} = 0$$ (2.4)

We shall consider each of these cases separately as different methods are required for each.