The system under investigation consists of an interacting region of
one or more quantum dots connected between leads or electron reservoirs of
specified chemical potential. In general the reservoirs will have different
chemical potentials, causing a current to flow through the dots. This makes
it inherently a non-equilibrium process. Therefore the system will be
best described using non-equilibrium Green's functions, now commonly
referred to as the Keldysh method [10, 11]. This formalism is not
only valid in the linear response regime, but also for higher bias
voltages. A full description not only requires knowledge of the retarded
and advanced Green's functions, as in equilibrium, but also of the
`distribution' Green's function ![]() between the reservoir and dot sites.
between the reservoir and dot sites.
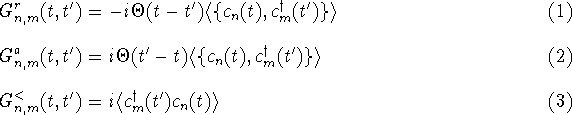
where ![]() and c are the usual creation and annihilation
operators.
In steady state the diagonal elements of
and c are the usual creation and annihilation
operators.
In steady state the diagonal elements of ![]() are
proportional to the local density of states, whereas
are
proportional to the local density of states, whereas
![]() plays the role of the density matrix.
They are related by the distribution matrix
plays the role of the density matrix.
They are related by the distribution matrix ![]() , defined by
, defined by
![]() . In equilibrium
. In equilibrium ![]() is
simply a scalar and is identical to the Fermi-Dirac distribution function.
is
simply a scalar and is identical to the Fermi-Dirac distribution function.
Having introduced the non-equilibrium Green's functions, the obvious
next step is to find an expression for the Landauer formula [12]
relating the current to the local properties of the system, such as the
chemical potentials of the reservoirs, the density of states and the average
occupation of the dots. It is assumed that the left and right electron
reservoirs are large enough to have well-defined Fermi-Dirac distributions,
![]() and
and ![]() , and chemical potentials
, and chemical potentials ![]() and
and ![]() . Any
interaction effects in the reservoirs can be neglected as a result of the
screening by the free flow of charge carriers.
Transport proceeds by electrons hopping between the reservoirs
and the interacting region. The Landauer formula can be written as [13]
. Any
interaction effects in the reservoirs can be neglected as a result of the
screening by the free flow of charge carriers.
Transport proceeds by electrons hopping between the reservoirs
and the interacting region. The Landauer formula can be written as [13]
![]()
where ![]() are matrices coupling the interacting
region to the reservoirs.
are matrices coupling the interacting
region to the reservoirs. ![]() are the hopping potentials between
the reservoirs and the interacting region and
are the hopping potentials between
the reservoirs and the interacting region and ![]() is the density
of states in the reservoirs.
It is worth noting that the Green's functions in this formula are to
be calculated from the full Hamiltonian including the reservoirs, even
though the reservoirs are already present in the couplings
is the density
of states in the reservoirs.
It is worth noting that the Green's functions in this formula are to
be calculated from the full Hamiltonian including the reservoirs, even
though the reservoirs are already present in the couplings ![]() of the current equation.
of the current equation.
For negligible bias voltages, knowledge of the retarded
(and hence the advanced) Green's functions allows the distribution Green's
functions to be calculated. The next step is to choose a particular Hamiltonian
H and to calculate the retarded Green's functions explicitly.
This can be done using the
equation of motion method which
consists of differentiating the Green's function with respect to
time, thus creating higher order Green's functions.
In Fourier space this amounts to the following
iteration rule (![]() ):
):
![]()
where ![]() can be any combination of different creation and
annihilation operators and
can be any combination of different creation and
annihilation operators and
![]() is the
Fourier transform of the retarded Green's function.
The above equation can be applied successively to
produce multiple particle Green's functions. For a system of two reservoirs and
N dots with n energy levels a multiple particle operator consists of a
product of at most 4 (n N+2)-1
single particle operators, i.e. the
creation and annihilation operators for both spin orientations in each dot
level or reservoir. Therefore, it is in principle possible to obtain a closed
set of equations. Clearly, it is a daunting task to calculate and solve all
possible simultaneous equations, so one usually resorts to making some
approximations in order to close the set of coupled equations.
is the
Fourier transform of the retarded Green's function.
The above equation can be applied successively to
produce multiple particle Green's functions. For a system of two reservoirs and
N dots with n energy levels a multiple particle operator consists of a
product of at most 4 (n N+2)-1
single particle operators, i.e. the
creation and annihilation operators for both spin orientations in each dot
level or reservoir. Therefore, it is in principle possible to obtain a closed
set of equations. Clearly, it is a daunting task to calculate and solve all
possible simultaneous equations, so one usually resorts to making some
approximations in order to close the set of coupled equations.