In order to determine
a realistic, yet simple, set of approximations, consider the simple case
of a single quantum dot where only one relevant level for each spin direction
will be taken into account. Any lower levels are assumed to
be permanently occupied and higher energy levels are always empty.
The two relevant states in the dot are labelled by the electron spin
quantum numbers 
or 
.
A tight binding Hamiltonian will be used with a Hubbard term U describing the
Coulomb interaction between the spin up and spin down electrons.
This is analogous to the Anderson model of localised impurity
states in metals [14].
where 
and 
are the single particle energy levels
in the dot and reservoirs respectively. Transport between dot and reservoir
proceeds by means of the hopping potential 
.
Any interaction that might take place with electrons in
the full lower energy levels is incorporated in the definition of
. The hopping potentials are taken to be real,
because of the time-reversal symmetry.
It is required that any set of approximations yields the correct solution
in the limit of zero bandwidth, i.e. negligible hopping potential. Moreover,
the single particle density of states integrated over all energies must
equal unity. The density of states must be non-negative at all energies.
Finally, the solution should display electron-hole symmetry. It should be
invariant under the transformation 
.
The crudest set of
approximations (scheme 1) consistent with these conditions
[15] corresponds to the
Hartree approximation scheme [16] where electrons of
opposite spin do not interact directly, but only through a modified
average potential field.
The resulting Green's function is
with
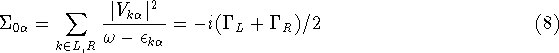
where 
.
is the self-energy due to the tunnelling of the electron
and 
is the average occupancy of the opposite
spin state. The same Green's function results from
the method as indicated by Caroli, Combescot and Nozieres [17],
where the full Green's function is calculated as a perturbation of the
system without transmission to either reservoir.
The occupation is the
integrated product of the (diagonal) distribution function and the local
density of
states in the dot. Since the Green's function is related to the density
of states which in turn depends on the average occupation number,
it means that equation
7 is to be solved self-consistently. It can be shown that the
integrated density of states equals unity, subject to the condition
, which is obviously satisfied in any
real system.
A better approximation scheme (scheme 2) is one which neglects the simultaneous
tunnelling of the electron of opposite spin, but which does not decouple the
higher order Green's functions as in approximation scheme 1.
This yields the following Green's function:
As the tunnelling of the opposite spin electron is not taken into account,
its creation and annihilation operators are always paired together in the
higher order Green's functions. The operators for both spins do not
truly intermingle, which results in the probabilistic expression for
the Green's function. Therefore, the same expression can be obtained by
solving the Green's function for the isolated site and adding an
imaginary part to the site energy to include the reservoirs, i.e. the
reservoirs simply serve as a source of broadening.
A more accurate method (scheme 3) only neglects terms involving correlation in
the leads, valid for temperatures higher than the Kondo temperature
[16].
The Green's function corresponding to these approximations is [3]
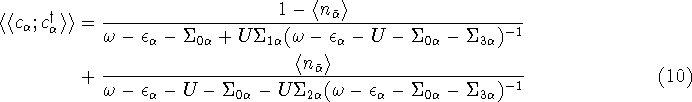
The self-energies due to the tunnelling of the electron
are defined as
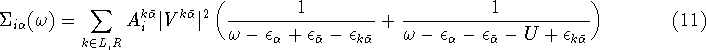
where 
, 
and 
.
As for scheme 2, it can be shown that the density of states integrates to
unity for all values of 
.
Since the couplings to the reservoirs differ by a constant factor
the distribution matrix reduces to a diagonal matrix.
As there is only one level for each spin
the current expression 4 takes an especially simple form
where the current is proportional
to the density of states between the Fermi levels of the reservoirs.
The Ohmic conductance is given by the integrated product of the
density of states and the derivative of the Fermi function.
At low temperatures the derivative of the Fermi function approximates
a 
-function. A Lorentzian density of states with its broadening
caused solely by tunnelling to and from the reservoirs thus gives rise to a
conductance peak of height 
, provided that the dot is symmetrically
coupled to the reservoirs.
The three approximation schemes are compared in figures 1-
3 for the case where the temperature equals the broadening due
to the reservoirs. In
order to distinguish between the electrons in the dot, a magnetic field is
applied giving rise to a Zeeman splitting of the energy levels (
).
Figure 1 shows the current and the associated differential
conductance through the dot when a bias voltage is applied across it, keeping
the chemical potential in the right reservoir fixed
(
). All three approximation schemes yield qualitatively the
same results, although scheme 3 (and scheme 2 to a lesser extent) has a
larger associated broadening. This is a direct consequence of the fact that
scheme 3 takes the tunnelling of the oppositely charged electron into account.
In figure 2 the Ohmic conductance is plotted. The approximation schemes give identical solutions for the shape and height of the major conductance peaks, but especially approximation scheme 1 gives a different result for the amplitude of the minor peaks. Moreover, an investigation of the occupation plot 3 shows that for scheme 1 the average occupation of the higher energy spin state can exceed that of the other spin state for intermediate values of the chemical potential of the reservoirs. This is clearly unphysical. Both these observations justify the conclusion that scheme 1 should be dismissed as a good set of approximations.
As expected the conductance plot shows peaks at the single particle energy
levels and at the same energies displaced by U. It is clear that two peaks
are suppressed, which can be explained as follows. The first peak occurs
when transport takes place through the lowest level .
As the chemical potential in the reservoirs is raised, the state
will start to fill up. When the chemical potential
lines up with
, level will be mostly occupied (see figure
3) thus putting the Coulomb blockade in place and impeding
the flow of electrons through level . This
results in a highly suppressed conductance peak. Because of the
electron-hole symmetry a similar situation occurs at much higher
values of the chemical potential.
Approximation schemes 2 and 3 seem to give results which are closely in accordance with each other. The main difference is that approximation scheme 3 produces a larger associated broadening. Although slightly better, scheme 3 is harder to manipulate numerically, whereas scheme 2 is much more stable. Therefore approximation scheme 2 will be employed here.