Introduction



Next: Transfer Matrix Calculations
Up: Critical Exponents for the
Previous: Critical Exponents for the
The metal-insulator transition in disordered systems has been the
subject of theoretical and experimental work at least since
Anderson (1958). The similarities with thermodynamic phase
transitions had been noted by several authors(Thouless 1974, Wegner 1976) but it
was not until 1979 that a usable formulation of the renormalisation
group or scaling theory became available (Abrahams et al. 1979, Wegner 1979, Efetov 1983).
The basic assumption of these theories, that the behaviour could be
described by a single parameter scaling theory, was confirmed in
numerical calculations by the present author (MacKinnon & Kramer 1981, MacKinnon & Kramer 1983). For
a recent review of the area see Kramer & MacKinnon (1993).
In spite of the progress made the exponents,  and
and  , describing
the behaviour of the conductivity and the localisation length
respectively have proven difficult to calculate reliably. For some
time there appeared to be a consensus between theory and experiment
that both exponents were equal to unity, but more recently this has
been called into question from both the theoretical
(e.g. Kravtsov & Lerner 1984, Lerner 1991) and from the experimental (Stupp et al. 1993)
side.
, describing
the behaviour of the conductivity and the localisation length
respectively have proven difficult to calculate reliably. For some
time there appeared to be a consensus between theory and experiment
that both exponents were equal to unity, but more recently this has
been called into question from both the theoretical
(e.g. Kravtsov & Lerner 1984, Lerner 1991) and from the experimental (Stupp et al. 1993)
side.
Numerical results have been scattered at least between 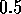 and
and 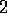 with numerous attempts at developing alternative methods of
calculation. A good example of the difficulties is given by the
contrast between calculations for the Anderson model with rectangular
or Gaussian disorder(Kramer et al. 1990). Using identical methods the
exponents obtained were about
with numerous attempts at developing alternative methods of
calculation. A good example of the difficulties is given by the
contrast between calculations for the Anderson model with rectangular
or Gaussian disorder(Kramer et al. 1990). Using identical methods the
exponents obtained were about 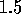 and
and 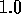 for the rectangular and
Gaussian distributions respectively. It is clearly unreasonable for
the exponents for these two cases to be different. In fact if they
were different then it would call into question the justification of
the use of any simple model Hamiltonian to describe the transition and
so undermine the whole foundation of the subject.
for the rectangular and
Gaussian distributions respectively. It is clearly unreasonable for
the exponents for these two cases to be different. In fact if they
were different then it would call into question the justification of
the use of any simple model Hamiltonian to describe the transition and
so undermine the whole foundation of the subject.
In this paper the results of calculations carried out over several
years are presented. All the basic results have an accuracy of at
least 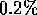 which enables the critical exponents to be calculated
much more accurately than when the conventional
which enables the critical exponents to be calculated
much more accurately than when the conventional 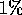 is used.
is used.



Next: Transfer Matrix Calculations
Up: Critical Exponents for the
Previous: Critical Exponents for the
Angus MacKinnon - Aonghas Mac Fhionghuin
Tue Nov 29 13:32:02 gmt 1994
 and
and  , describing
the behaviour of the conductivity and the localisation length
respectively have proven difficult to calculate reliably. For some
time there appeared to be a consensus between theory and experiment
that both exponents were equal to unity, but more recently this has
been called into question from both the theoretical
(e.g. Kravtsov & Lerner 1984, Lerner 1991) and from the experimental (Stupp et al. 1993)
side.
, describing
the behaviour of the conductivity and the localisation length
respectively have proven difficult to calculate reliably. For some
time there appeared to be a consensus between theory and experiment
that both exponents were equal to unity, but more recently this has
been called into question from both the theoretical
(e.g. Kravtsov & Lerner 1984, Lerner 1991) and from the experimental (Stupp et al. 1993)
side.
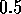 and
and 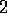 with numerous attempts at developing alternative methods of
calculation. A good example of the difficulties is given by the
contrast between calculations for the Anderson model with rectangular
or Gaussian disorder(
with numerous attempts at developing alternative methods of
calculation. A good example of the difficulties is given by the
contrast between calculations for the Anderson model with rectangular
or Gaussian disorder(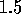 and
and 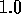 for the rectangular and
Gaussian distributions respectively. It is clearly unreasonable for
the exponents for these two cases to be different. In fact if they
were different then it would call into question the justification of
the use of any simple model Hamiltonian to describe the transition and
so undermine the whole foundation of the subject.
for the rectangular and
Gaussian distributions respectively. It is clearly unreasonable for
the exponents for these two cases to be different. In fact if they
were different then it would call into question the justification of
the use of any simple model Hamiltonian to describe the transition and
so undermine the whole foundation of the subject.
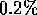 which enables the critical exponents to be calculated
much more accurately than when the conventional
which enables the critical exponents to be calculated
much more accurately than when the conventional 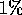 is used.
is used.