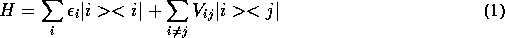
The transfer matrix method has been discussed in numerous papers (MacKinnon & Kramer 1983, Pichard & Sarma 1981) so only the briefest outline will be attempted here.
The starting point is the usual Anderson (1958) Hamiltonian
where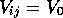 
between nearest neighbours on a simple cubic
lattice and zero otherwise. In this work 
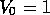is chosen and will
therefore not be mentioned explicitly. The diagonal elements
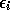are independent random numbers chosen either from a
uniform rectangular distribution with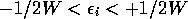 
or from a Gaussian distribution of standard deviation 
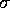. For
purposes of comparison between the two cases an effective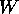 
for the
Gaussian case may be defined by equating the variances as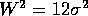 
.
In terms of the coefficients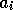 
of the wavefunctions on each site the
Schrödinger equation may be written in the form
Consider now a long bar composed of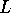 
slices of cross-section
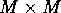. By combining the 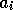s from each slice into a vector
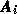(2) can be written in the concise form
where the subscripts 
now refer to slices and matrix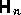 
is
the Hamiltonian for slice . By rearranging (3) the
transfer matrix is obtained
A theorem attributed to Oseledec (1968) states that
where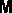 
is a well defined matrix and 
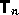are products of
random matrices. The logarithms of the eigenvalues of 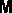are
referred to as Lyapunov exponents and occur in pairs which are
reciprocals of one another. By comparison with (4) the
Lyapunov exponents may be identified with the rate of exponential rise
(or fall) of the wave functions. In fact the smallest exponent
corresponds to the longest decay length and hence to the localisation
length of the system.
In principle then it is necessary to calculate 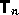for large
, and diagonalise 
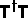. Unfortunately the
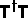calculation is not quite so simple: the different eigenvalues of rise at different rates so that the smallest, which we
seek, rapidly becomes insignificant compared to the largest and is lost
in the numerical rounding error. Typically this happens after about 10
steps.
