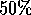 or
or 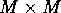 vectors rather than the full
vectors rather than the full 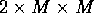 as the required vector is invariably the
as the required vector is invariably the 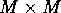 th.
th.
In order to obtain the smallest Lyapunov exponent it is necessary to overcome this loss of numerical significance. This can be achieved in more than one way of which the orthogonalisation method is employed here.
After about 10 matrices have been multiplied together the columns of the product matrix are orthogonalised to each other and normalised. This is equivalent to multiplying the product from the right by an appropriate matrix. This orthonormalisation process automatically separates the different exponentially growing contributions.
The process is repeated every 10 or so steps and the logarithm of the
length of the vector closest to unity is stored. The Lyapunov exponent
is given by the mean value of these logarithms divided by the number of
steps between orthonormalisations. In practice it is necessary to use
only 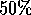 or
or 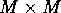 vectors rather than the full
vectors rather than the full 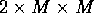 as the required vector is invariably the
as the required vector is invariably the 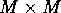 th.
th.
The error in the Lyapunov exponent can be estimated from the variance corresponding to the mean exponent. Although this estimate could be biased by correlations between the different contributions this is not found to be a serious problem in practice, at least when the localisation length is short compared with the distance between orthogonalisation steps.
The optimum frequency of orthogonalisation steps can be estimated by
comparing the length of the 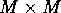 th vector before and after
orthogonalisation. The ratio should not be allowed to get close to the
machine accuracy.
th vector before and after
orthogonalisation. The ratio should not be allowed to get close to the
machine accuracy.