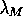 . The renormalised length
. The renormalised length 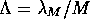 is
found to obey a scaling theory(MacKinnon & Kramer 1981, MacKinnon & Kramer 1983) such that
is
found to obey a scaling theory(MacKinnon & Kramer 1981, MacKinnon & Kramer 1983) such that
The inverse of the smallest Lyapunov exponent is the localisation
length 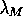 . The renormalised length
. The renormalised length 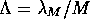 is
found to obey a scaling theory(MacKinnon & Kramer 1981, MacKinnon & Kramer 1983) such that
is
found to obey a scaling theory(MacKinnon & Kramer 1981, MacKinnon & Kramer 1983) such that
which has solutions of the form
where 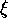 is a characteristic length scale which can be identified
with the localisation length of the insulator and which scales as the
reciprocal of the resistivity of the metallic phase(MacKinnon & Kramer 1983).
is a characteristic length scale which can be identified
with the localisation length of the insulator and which scales as the
reciprocal of the resistivity of the metallic phase(MacKinnon & Kramer 1983).
In 3D (6) always has a fixed point 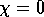 which corresponds
to the metal-insulator transition. The behaviour close to the
transition can be found by linearising (6) and solving to
obtain
which corresponds
to the metal-insulator transition. The behaviour close to the
transition can be found by linearising (6) and solving to
obtain
where  is the disorder
is the disorder 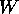 or
or 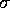 ,
, 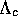 and
and 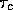 represent the critical
represent the critical 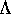 and disorder respectively, and
and disorder respectively, and 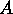 and
and
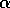 are constants. By comparing (7) and (8) an
expression for
are constants. By comparing (7) and (8) an
expression for 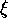 can be obtained in the form
can be obtained in the form
so that the localisation length exponent  is given by
is given by 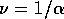 . Since it is well known(Wegner 1976, Abrahams et al. 1979) that the
conductivity exponent
. Since it is well known(Wegner 1976, Abrahams et al. 1979) that the
conductivity exponent  is related to
is related to  by
by 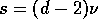 then by
fitting (8) to the data and calculating
then by
fitting (8) to the data and calculating 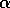 both exponents
can be obtained.
both exponents
can be obtained.