One simple feature of (8) is that, when 
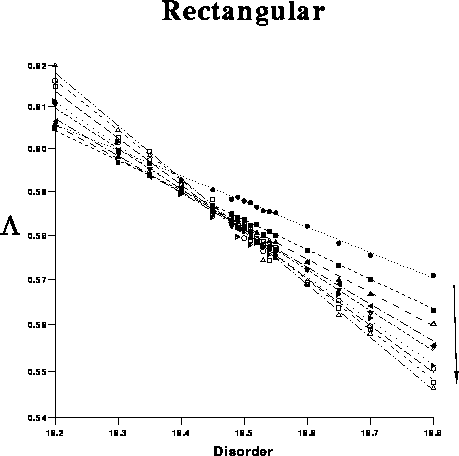
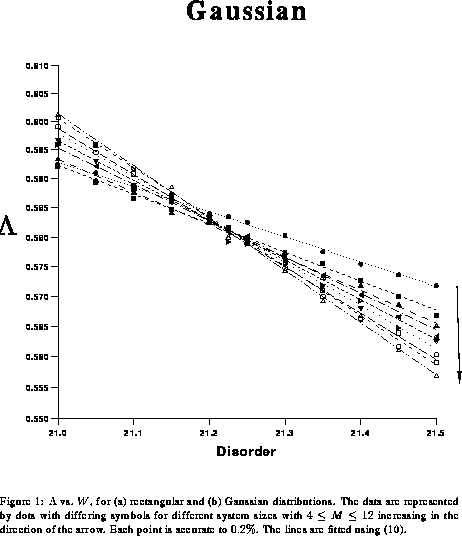
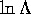is
plotted against 
, the curves for different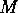 
intersect at a
common point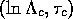 
. In practice the data do not
behave in exactly this way. There is a small deviation from scaling.
This deviation could be taken into account by adding an extra term to
(8) which depends on 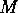but not on . Consider, however,
the form
which represents the most general form of such a correction. If a
specific form for the correction were assumed it would require at least
4 independent fitting parameters to represent 
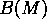, including
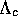and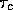 
, and may still not represent the true deviation
from scaling. It seems better therefore to fit an independent
for each value of and therefore to make no assumption about the
nature of the deviation from scaling, other than that it is
non-critical, and therefore independent of , in the region of
interest. By fitting the data to (10) in this way the
exponent 
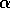is derived solely from the gradient of
vs. and the intercept is allowed to float. The results of
such fits are shown in figure 1.
