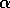 . The quality of the fit can be tested by computing
. The quality of the fit can be tested by computing 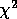 defined as
defined as
The data can be fitted to (10) by iteratively using a standard
least squares procedure. Care is required with the non-linear parameter
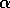 . The quality of the fit can be tested by computing
. The quality of the fit can be tested by computing 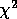 defined as
defined as
where 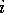 runs over all data points and
runs over all data points and 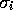 is the error in
point
is the error in
point 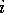 . After fitting
. After fitting 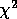 should be approximately equal to the
number of data points less the number of fitted parameters. Hence the
value of
should be approximately equal to the
number of data points less the number of fitted parameters. Hence the
value of 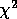 provides a measure of the quality of the fit. In
the results presented here the range of values of disorder round the
critical value was chosen such that
provides a measure of the quality of the fit. In
the results presented here the range of values of disorder round the
critical value was chosen such that 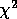 conforms to this
condition. Then a large number of additional points was calculated
inside this range. An important side effect of this procedure is that
the apparently acceptable range of disorder around the fixed point gets
narrower
as the calculations become more accurate. It is therefore important to
test whether any apparent change in the fitted exponent is due to this
narrowing.
conforms to this
condition. Then a large number of additional points was calculated
inside this range. An important side effect of this procedure is that
the apparently acceptable range of disorder around the fixed point gets
narrower
as the calculations become more accurate. It is therefore important to
test whether any apparent change in the fitted exponent is due to this
narrowing.
The values of the ideal and the fitted 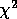 as well as the range
considered are shown in table 1. Using
as well as the range
considered are shown in table 1. Using 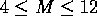 and the
widest range of disorder
and the
widest range of disorder 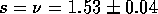 and
and 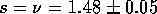 for rectangular and Gaussian cases respectively.
for rectangular and Gaussian cases respectively.