Percolation remains a very active field of research, both numerically and analytically.
Large scale computer simulations are constrained by CPU power
and memory. The Hoshen Kopelman algorithm [1] together with Nakanishi label
recycling [2] relaxes the
latter constraint by requiring memory of order
O(Ld-1) - rather than O(Ld) - where L
is the system size and d is the dimension.
However, histogram data (cluster size distributions, largest cluster distributions, etc.)
still require O(Ld) memory, and large scale simulations
often require parallelisation in order to produce results within a reasonable time.
We have implemented a parallelised algorithm which, in principle, relaxes all
constraints on networks, CPU power, and the memory of `slave' nodes [3].
We now describe the algorithm for d = 2 and present some results.
Description
A lattice is decomposed into squares which are independently realised by slave nodes.
Once a node finishes realising its lattice using the Hoshen Kopelman
algorithm, it sends a specially prepared version of the lattice border configuration
(rather than the whole lattice) to the master node. The master node
asynchronously receives lattices and glues them together as patches to form a superlattice:
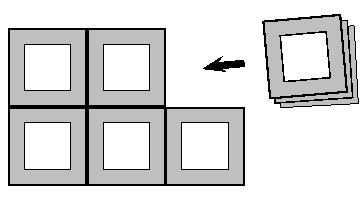
Figure 1: A superlattice is constructed by combining the borders of individual patch lattices.
These patch lattices will generally be rotated, mirrored and permuted.
The master node's responsibilities include the following:
- Receiving and combining lattice boundaries (see Fig. 1).
- Accounting for interlattice clusters (see Fig. 2).
- Combining histograms.
- Checking for percolating clusters, applying boundary conditions, etc.
The key to this algorithm is the representation of the lattice borders by the slave nodes.
We encode all information about size and connectivity explicitly in the border sites.
This is essentially a form of Nakanishi label recycling where border sites
are considered active and bulk sites not connected to border sites are considered inactive.
The slave node scans the border of the lattice it generates,
and writes the size of a cluster (as a negative number) in one of the cluster's sites.
All other sites in this cluster point to this root site. Clusters in the
bulk have their sizes recorded in a histogram.
When two patches are combined by the master it is possible that
the common border allows an interlattice cluster to extend between the patches. The master node
recognises this by a site-to-site comparison of the border.
To produce the correct statistics for interlattice clusters, the original cluster sizes must be deleted
from the histogram and replaced by their sum.
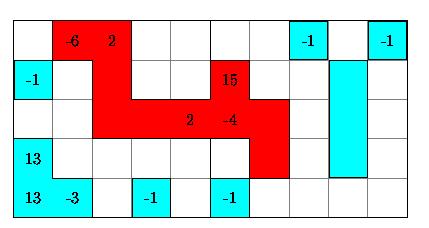
Figure 2: Two lattices have been glued together to form a superlattice.
A cluster in the middle crosses the border separating the original lattices.
In the above case the master node would therefore perform:
hist[6] = -1
hist[4] = -1
hist[6+4] = +1
Since histograms are superimposable, they may be stored locally
within the slave node until the entire simulation has finished. Boundary conditions may be
applied and percolating clusters identified by scanning the perimeter of
the superlattice and checking for common labels. Patches may be combined so as
to produce superlattices of different aspect ratios.
To improve statistics we can rotate, mirror and permute a set of patches randomly.
Results
We present some preliminary results for superlattices of
different aspect ratios with constant area 3000 by 3000.
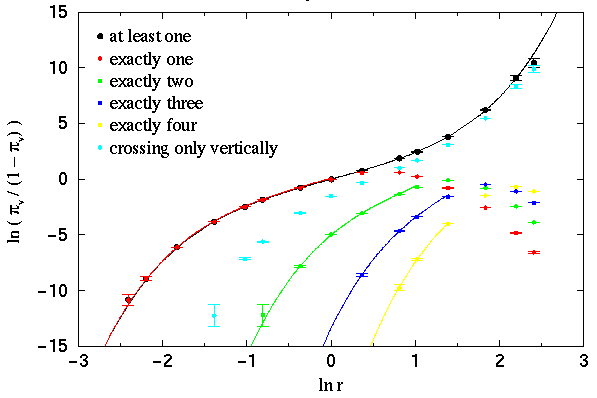
Figure 3: Probability of a crossing cluster.
The black points plot the probability of finding at least one vertical
crossing cluster, piv, for different aspect ratios,
where r = width/height. The curved black line is given
by Cardy's [4],
The coloured points plot the probability of finding exactly 1, 2, 3 or 4
vertical crossing clusters for different aspect ratios.
The curved coloured lines are conjectured by
Cardy [5] to be valid for small r.
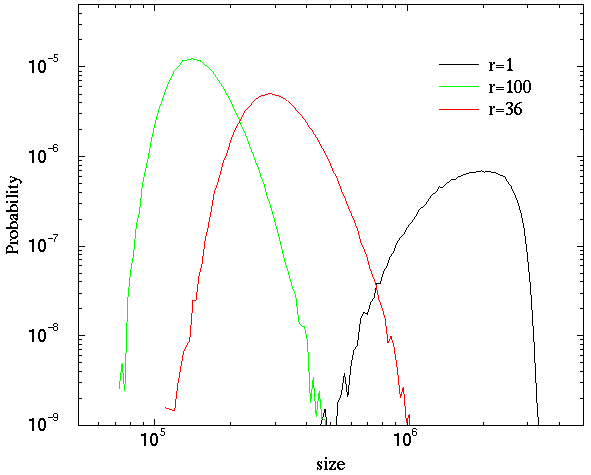
Figure 4: The histograms plot the size of spanning
clusters [6] for three different aspect ratios, r = 1, 36, 100.
Discussion
If a master node is too slow in combining patches it can only
serve a small number of slave nodes - another master node should share the burden.
If a master node is too quick in combining patches the rate of arrival of patches
should be increased. There is therefore an optimal master to slave node ratio
where the master combines patches as fast as they arrive.
If this ratio is unity then each slave has its own master and the whole scheme reduces to a way of
recycling a single lattice to produce results for different aspect ratios.
We note that a node scales as O(Ld) in time for producing a patch
lattice, while a master node scales as O(Ld-1) in time for
gluing lattices together. In this way it is possible to tune the above ratio by
adjusting the size of the patch lattice.
Conclusion
The method we have implemented relaxes the typical constraints on simulating
percolation and even works for slow computers served by a slow network.
Systems of enormous size can be simulated within a reasonable time.
The algorithm makes use of the following key features:
- The asynchronous nature of superlattice construction - it does
not matter when or whence a patch lattice arrives.
- Two-dimensional decomposition by using a compact representation of a patch lattice border.
- The superimposability of histograms across patches.
Our method is particularly well suited for studying spanning and wrapping clusters for different aspect ratios.
The machines we used to produce our preliminary results belong to the
undergraduate teaching sections and are entirely idle outside working hours.
Hitherto they ran screen savers during the night. They performed our algorithm
instead, and comfortably beat the world record for the largest
percolation simulation (4 million by 4 million), set by a
Cray T3E [7] a year ago. Our record now stands at 22.2 million by 22.2 million,
which represents about 500 trillion random number calls!
References
[1] J. Hoshen and R. Kopelman,
Percolation and cluster distribution. I. cluster multiple labeling technique and
critical ...,
Phys. Rev. B 14, 3438-3445 (1976).
[2] H. Nakanishi and H.E. Stanley,
Scaling studies of percolation phenomena in systems of dimensionality 2 to 7: Cluster numbers.
Phys. Rev. B 22, 2466-2488 (1980).
[3] Nicholas R. Moloney and Gunnar Pruessner,
Asynchronously Parallelized Percolation on Distributed Machines,
Phys. Rev. E67 037701 (2003).
[4] J.L. Cardy,
Critical percolation in finite geometries ,
J. Phys. A 25, L201-L206, (1992).
[5] J.L. Cardy,
The number of incipient spanning clusters in two-dimensional percolation,
J. Phys A 31, L105-L110 (1998).
[6] S.T. Bramwell et al.,
Universal fluctuations in correlated systems,
Phys. Rev. Lett. 84, 17 (2000).
[7] D. Tiggemann,
Simulation of percolation on massively-parallel computers,
Int. J. Mod. Phys. C 12, 871 (2001).
[8] Gunnar Pruessner and Nicholas R. Moloney,
Numerical results for crossong, spanning and wrapping in two-dimensional percolation,
J. Phys. A 36 11213 (2003).
[ Home ][ Research
interests ]




