


Next: 5.4 Overlap matrix elements
Up: 5. Localised basis-set
Previous: 5.2 Origin of the
Contents
We define the Fourier transform of a basis function
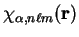 by
by
The angular integral is performed by using the expansion of
![$\exp[{\mathrm{i}} {\bf k} \cdot {\bf r}]$](img636.gif) into spherical-waves
(A.3, appendix A) leaving the radial integral
into spherical-waves
(A.3, appendix A) leaving the radial integral
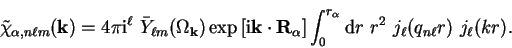 |
(5.8) |
The radial integral can now be calculated using equations
A.4 and A.5 and the
boundary conditions (that the basis functions are finite at 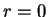 and vanish at
and vanish at
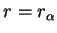 ) for the cases when
) for the cases when
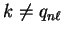 and
and
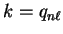 respectively. The final result for the
Fourier transform of a basis function is then
respectively. The final result for the
Fourier transform of a basis function is then
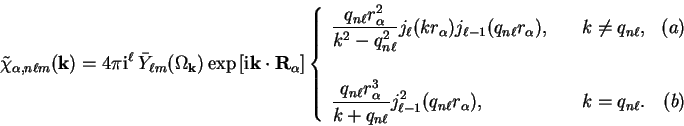 |
(5.9) |
Equation 5.9b is in fact a limiting case of
(5.9a) which can therefore always be substituted for
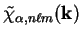 in an integral over
reciprocal-space.
in an integral over
reciprocal-space.



Next: 5.4 Overlap matrix elements
Up: 5. Localised basis-set
Previous: 5.2 Origin of the
Contents
Peter Haynes
![]() by
by