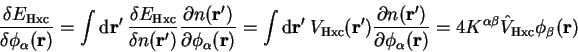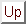


Next: 7.3 Penalty functional and
Up: 7. Computational implementation
Previous: 7.1 Total energy and
Contents
Subsections
7.2 Energy gradients
Having calculated the total energy, both the density-kernel
 and the expansion coefficients for the localised orbitals
and the expansion coefficients for the localised orbitals
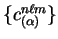 are varied. Because of the non-orthogonality
of the support functions, it is necessary to take note of the tensor
properties of the gradients [163], as noted in section 4.6.
are varied. Because of the non-orthogonality
of the support functions, it is necessary to take note of the tensor
properties of the gradients [163], as noted in section 4.6.
The total energy depends upon
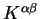 both explicitly and through the
electronic density
both explicitly and through the
electronic density 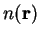 . We use the result
. We use the result
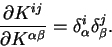 |
(7.20) |
From equations 7.6, 7.16 and 7.18 we have that
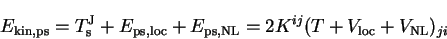 |
(7.21) |
and therefore
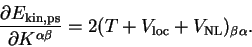 |
(7.22) |
The sum of the Hartree and exchange-correlation energies,
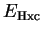 depends only on the density so that
depends only on the density so that
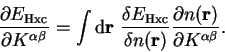 |
(7.23) |
The functional derivative of the Hartree-exchange-correlation energy with
respect to the electronic density is simply the sum of the Hartree and
exchange-correlation potentials,
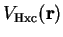 . The
electronic density is given in terms of the density-kernel by
. The
electronic density is given in terms of the density-kernel by
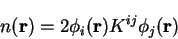 |
(7.24) |
so that we obtain
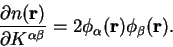 |
(7.25) |
Finally, therefore
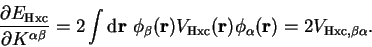 |
(7.26) |
Defining the matrix elements of the Kohn-Sham Hamiltonian in the representation
of the support functions by
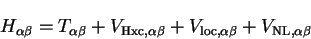 |
(7.27) |
the derivative of the total energy with respect to the density-kernel is
simply
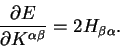 |
(7.28) |
Again we can treat the kinetic and pseudopotential energies together,
and the Hartree and exchange-correlation energies together. We use the
result that
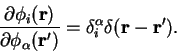 |
(7.29) |
We define the kinetic energy operator
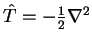 , whose matrix elements are
, whose matrix elements are
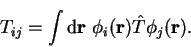 |
(7.30) |
Since the operator is Hermitian,
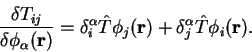 |
(7.31) |
Therefore
The derivation for the pseudopotential energy is identical with the
replacement of 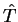 by the pseudopotential operator, and so the result
for the sum of these energies is just
by the pseudopotential operator, and so the result
for the sum of these energies is just
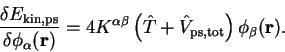 |
(7.33) |
Again this gradient is derived by considering the change in the
electronic density.
![\begin{displaymath}
\frac{\partial n({\bf r'})}{\partial \phi_{\alpha}({\bf r})}...
..._i({\bf r'}) \delta({\bf r} - {\bf r'}) K^{i \alpha} \biggr] .
\end{displaymath}](img986.gif) |
(7.34) |
Therefore
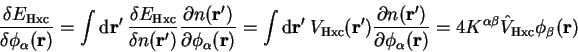 |
(7.35) |
The gradient of the total energy with respect to changes in the
support functions is
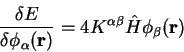 |
(7.36) |
where 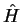 is the Kohn-Sham Hamiltonian which operates on
is the Kohn-Sham Hamiltonian which operates on
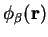 .
.



Next: 7.3 Penalty functional and
Up: 7. Computational implementation
Previous: 7.1 Total energy and
Contents
Peter Haynes
![]() and the expansion coefficients for the localised orbitals
and the expansion coefficients for the localised orbitals
![]() are varied. Because of the non-orthogonality
of the support functions, it is necessary to take note of the tensor
properties of the gradients [163], as noted in section 4.6.
are varied. Because of the non-orthogonality
of the support functions, it is necessary to take note of the tensor
properties of the gradients [163], as noted in section 4.6.
![]() both explicitly and through the
electronic density
both explicitly and through the
electronic density ![]() . We use the result
. We use the result
![]() depends only on the density so that
depends only on the density so that
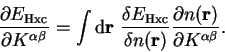
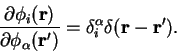
![]() , whose matrix elements are
, whose matrix elements are
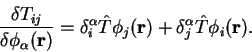
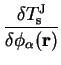
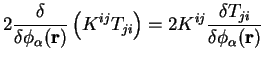
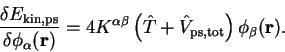
![\begin{displaymath}
\frac{\partial n({\bf r'})}{\partial \phi_{\alpha}({\bf r})}...
..._i({\bf r'}) \delta({\bf r} - {\bf r'}) K^{i \alpha} \biggr] .
\end{displaymath}](img986.gif)