


Next: 7.6 Tensor properties of
Up: 7. Computational implementation
Previous: 7.4 Physical interpretation
Contents
7.5 Occupation number preconditioning
The eigenvalues of the Hessian at a stationary point determine the nature
and shape of that stationary point. Thus the shape of the ground-state
minimum of an energy functional is determined by the eigenvalues of that
functional. For the Kohn-Sham scheme these eigenvalues are the
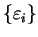 and the narrower the eigenvalue spectrum, the more
``spherical'' the minimum, and the easier the functional is to minimise.
From equation 4.9 we note that when partial occupation
numbers are
introduced, the relevant eigenvalue spectrum becomes
and the narrower the eigenvalue spectrum, the more
``spherical'' the minimum, and the easier the functional is to minimise.
From equation 4.9 we note that when partial occupation
numbers are
introduced, the relevant eigenvalue spectrum becomes
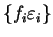 .
When conduction bands are included in a calculation, their occupation numbers
will be vanishingly small near the ground-state minimum, which will therefore be
very aspherical, and convergence of these bands will become very slow.
This problem has been addressed in the study of metallic systems
[164,165] by the method of preconditioning which
changes the metric of the parameter space to compress the eigenvalue
spectrum and make the minimum more spherical.
.
When conduction bands are included in a calculation, their occupation numbers
will be vanishingly small near the ground-state minimum, which will therefore be
very aspherical, and convergence of these bands will become very slow.
This problem has been addressed in the study of metallic systems
[164,165] by the method of preconditioning which
changes the metric of the parameter space to compress the eigenvalue
spectrum and make the minimum more spherical.
With reference to the results in appendix B,
we introduce a metric, represented by the matrix 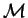 ,
such that a new set of
variables (denoted by a tilde) is introduced:
,
such that a new set of
variables (denoted by a tilde) is introduced:
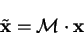 |
(7.53) |
and so that the new gradients are related to the old gradients by
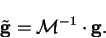 |
(7.54) |
In the new metric, the conjugate directions are defined (see appendix B) by
where we have adopted the Fletcher-Reeves method (B.22) for
calculating 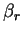 .
The line minimum is given by
.
The line minimum is given by
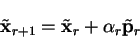 |
(7.57) |
which can be rewritten in terms of the original variables as
This identifies
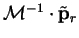 as the set of preconditioned
conjugate gradients for the original variables in the original space.
These directions
as the set of preconditioned
conjugate gradients for the original variables in the original space.
These directions
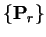 are thus given by
are thus given by
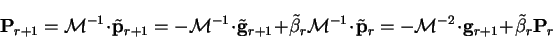 |
(7.59) |
so that the gradients to be used for the preconditioned search are
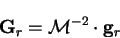 |
(7.60) |
with mixing factor
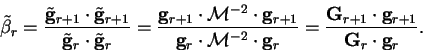 |
(7.61) |
It is observed that defining
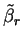 in terms of the
preconditioned gradients alone does not interfere with the minimisation
procedure, so that in practice
in terms of the
preconditioned gradients alone does not interfere with the minimisation
procedure, so that in practice
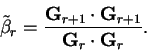 |
(7.62) |
In order to apply this scheme here, we choose to make the metric 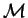 diagonal
in the representation of the Kohn-Sham orbitals. In the original variables
diagonal
in the representation of the Kohn-Sham orbitals. In the original variables
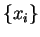 (the subscript
(the subscript 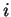 labels a component of a vector)
the minimum can be expanded as
labels a component of a vector)
the minimum can be expanded as
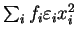 so that the scaled variables
so that the scaled variables
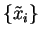 defined by
defined by
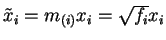 (where
(where
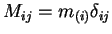 )
produce the desired compression since in terms of the new variables, the
minimum has the form
)
produce the desired compression since in terms of the new variables, the
minimum has the form
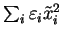 .
In the representation of the Kohn-Sham orbitals, the gradient of the functional
.
In the representation of the Kohn-Sham orbitals, the gradient of the functional
![$Q[\rho;\alpha]$](img1000.gif) (7.52) becomes
(7.52) becomes
![\begin{displaymath}
4 m_{(i)}^{-2}
\left[ f_i \left\{ {\hat H} -\varepsilon_i ...
...})
= 4 \left[ {\hat H} - \varepsilon_i \right]
\psi_i({\bf r})
\end{displaymath}](img1045.gif) |
(7.63) |
in which we see that the factor of 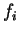 in front of the
in front of the 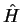 operator has been cancelled so that the effect of the gradient is now the
same on both occupied and unoccupied bands, and these bands should now
converge at the same rate.
operator has been cancelled so that the effect of the gradient is now the
same on both occupied and unoccupied bands, and these bands should now
converge at the same rate.
We now transform the preconditioned gradient back to the support function
representation using
![\begin{displaymath}
\frac{\delta Q[\rho;\alpha]}{\delta \phi_{\alpha}({\bf r})} ...
...alpha i} \frac{\delta Q[\rho;\alpha]}{\delta \psi_i({\bf r})}
\end{displaymath}](img1046.gif) |
(7.64) |
where
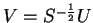 from 4.78 and
from 4.78 and 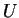 is a unitary
matrix.
Thus the preconditioned gradient we require is
is a unitary
matrix.
Thus the preconditioned gradient we require is
![\begin{displaymath}
4 V_{\alpha i} \left[ {\hat H} + \alpha f_i (1 - f_i)
(1 - 2...
...SK)(1-2SK)\right)^{\alpha \beta} \right] \phi_{\beta}({\bf r})
\end{displaymath}](img1047.gif) |
(7.65) |
from the properties of the matrix 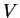 (4.79, 4.80).
We see that the gradient has thus been pre-multiplied by the matrix
(4.79, 4.80).
We see that the gradient has thus been pre-multiplied by the matrix 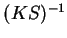 i.e. in the support function representation, the metric
i.e. in the support function representation, the metric 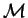 is
is
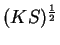 .
.
Although the overlap matrix 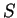 is a sparse matrix for localised support
functions, its inverse
is a sparse matrix for localised support
functions, its inverse 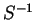 is not sparse in general, so that this scheme is
not straightforward to implement.
For a sufficiently diagonally dominant overlap matrix, it is possible to
approximate the inverse in the following manner. We write
is not sparse in general, so that this scheme is
not straightforward to implement.
For a sufficiently diagonally dominant overlap matrix, it is possible to
approximate the inverse in the following manner. We write 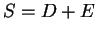 where
where  contains only the diagonal elements of
contains only the diagonal elements of  and
and 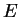 contains
the off-diagonal elements.
contains
the off-diagonal elements. 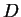 is thus trivial to diagonalise.
Writing
is thus trivial to diagonalise.
Writing
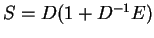 we have
we have
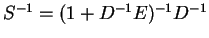 and if
and if 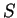 is diagonally dominant, the elements of the matrix
is diagonally dominant, the elements of the matrix
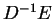 are small so that we can approximate the inverse of the term in
brackets. If the elements of a matrix
are small so that we can approximate the inverse of the term in
brackets. If the elements of a matrix 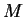 are small then
are small then
When the first few terms of equation 7.66 are applied to the
inverse overlap matrix we obtain
This expression could be used to obtain a good approximation to the inverse
overlap matrix, which may be sufficient for preconditioning, but there is
the danger that, particularly for large systems, the overlap matrix may
become singular and the performance of the algorithm would deteriorate.
In the following section, however, we show that the correct preconditioned
gradient does not involve the inverse of the overlap matrix.



Next: 7.6 Tensor properties of
Up: 7. Computational implementation
Previous: 7.4 Physical interpretation
Contents
Peter Haynes
![]() and the narrower the eigenvalue spectrum, the more
``spherical'' the minimum, and the easier the functional is to minimise.
From equation 4.9 we note that when partial occupation
numbers are
introduced, the relevant eigenvalue spectrum becomes
and the narrower the eigenvalue spectrum, the more
``spherical'' the minimum, and the easier the functional is to minimise.
From equation 4.9 we note that when partial occupation
numbers are
introduced, the relevant eigenvalue spectrum becomes
![]() .
When conduction bands are included in a calculation, their occupation numbers
will be vanishingly small near the ground-state minimum, which will therefore be
very aspherical, and convergence of these bands will become very slow.
This problem has been addressed in the study of metallic systems
[164,165] by the method of preconditioning which
changes the metric of the parameter space to compress the eigenvalue
spectrum and make the minimum more spherical.
.
When conduction bands are included in a calculation, their occupation numbers
will be vanishingly small near the ground-state minimum, which will therefore be
very aspherical, and convergence of these bands will become very slow.
This problem has been addressed in the study of metallic systems
[164,165] by the method of preconditioning which
changes the metric of the parameter space to compress the eigenvalue
spectrum and make the minimum more spherical.
![]() ,
such that a new set of
variables (denoted by a tilde) is introduced:
,
such that a new set of
variables (denoted by a tilde) is introduced:
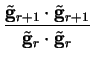
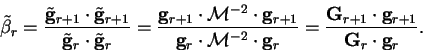
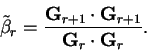
![]() diagonal
in the representation of the Kohn-Sham orbitals. In the original variables
diagonal
in the representation of the Kohn-Sham orbitals. In the original variables
![]() (the subscript
(the subscript ![]() labels a component of a vector)
the minimum can be expanded as
labels a component of a vector)
the minimum can be expanded as
![]() so that the scaled variables
so that the scaled variables
![]() defined by
defined by
![]() (where
(where
![]() )
produce the desired compression since in terms of the new variables, the
minimum has the form
)
produce the desired compression since in terms of the new variables, the
minimum has the form
![]() .
In the representation of the Kohn-Sham orbitals, the gradient of the functional
.
In the representation of the Kohn-Sham orbitals, the gradient of the functional
![]() (7.52) becomes
(7.52) becomes
![\begin{displaymath}
\frac{\delta Q[\rho;\alpha]}{\delta \phi_{\alpha}({\bf r})} ...
...alpha i} \frac{\delta Q[\rho;\alpha]}{\delta \psi_i({\bf r})}
\end{displaymath}](img1046.gif)
![]() is a sparse matrix for localised support
functions, its inverse
is a sparse matrix for localised support
functions, its inverse ![]() is not sparse in general, so that this scheme is
not straightforward to implement.
For a sufficiently diagonally dominant overlap matrix, it is possible to
approximate the inverse in the following manner. We write
is not sparse in general, so that this scheme is
not straightforward to implement.
For a sufficiently diagonally dominant overlap matrix, it is possible to
approximate the inverse in the following manner. We write ![]() where
where ![]() contains only the diagonal elements of
contains only the diagonal elements of ![]() and
and ![]() contains
the off-diagonal elements.
contains
the off-diagonal elements. ![]() is thus trivial to diagonalise.
Writing
is thus trivial to diagonalise.
Writing
![]() we have
we have
![]() and if
and if ![]() is diagonally dominant, the elements of the matrix
is diagonally dominant, the elements of the matrix
![]() are small so that we can approximate the inverse of the term in
brackets. If the elements of a matrix
are small so that we can approximate the inverse of the term in
brackets. If the elements of a matrix ![]() are small then
are small then