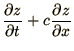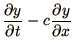Next: A Simple Algorithm
Up: Partial Differential Equations
Previous: Elliptic Equations
Hyperbolic Equations -- Wave equations
The classical example of a hyperbolic equation is the wave equation
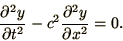 |
(2.5) |
The wave equation can be rewritten in the form
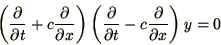 |
(2.6) |
or as a system of 2 equations
Note that the first of these equations (2.3a) is
independent of 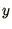 and can be solved on it's own. The second equation
(2.3b) can then be solved by using the known solution of the
first. Note that we could equally have chosen the equations the other
way round, with the signs of the velocity
and can be solved on it's own. The second equation
(2.3b) can then be solved by using the known solution of the
first. Note that we could equally have chosen the equations the other
way round, with the signs of the velocity 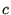 interchanged.
As the 2 equations (2.3) are so similar we expect the stability properties to
be the same. We therefore concentrate on (2.3a) which is
known as the Advective equation and is in fact the conservation
of mass equation of an
incompressible fluid
interchanged.
As the 2 equations (2.3) are so similar we expect the stability properties to
be the same. We therefore concentrate on (2.3a) which is
known as the Advective equation and is in fact the conservation
of mass equation of an
incompressible fluid
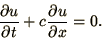 |
(2.9) |
Note also that the boundary conditions will usually be specified in the
form
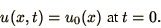 |
(2.10) |
which gives the value of 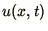 for all
for all 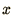 at a particular time.
at a particular time.
Subsections



Next: A Simple Algorithm
Up: Partial Differential Equations
Previous: Elliptic Equations