


Next: An Improved Algorithm
Up: Hyperbolic Equations
Previous: Hyperbolic Equations
As a first attempt to solve (2.9) we consider using centred
differences for the space derivative and Euler's method for the time
part
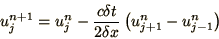 |
(2.11) |
where the subscripts 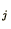 represent space steps and the superscripts
represent space steps and the superscripts
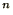 time steps. By analogy with the discussion of the
Euler and
Leap-Frog methods we can see
immediately that this method is 1st order accurate in
time steps. By analogy with the discussion of the
Euler and
Leap-Frog methods we can see
immediately that this method is 1st order accurate in 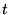 and 2nd order
in
and 2nd order
in 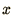 . We note firstly that
. We note firstly that
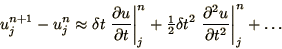 |
(2.12) |
whereas
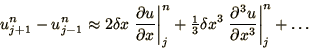 |
(2.13) |
and substitute these forms into (2.11) to obtain
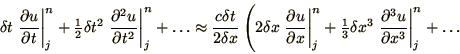 |
(2.14) |
so that, when the original differential equation (2.9) is
subtracted, we are left with a truncation error which is 2nd order in
the time but 3rd order in the spatial part.
The stability is a property of the time, 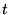 , integration rather than
the space,
, integration rather than
the space, 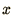 . We analyse this by considering a plane wave solution
for the
. We analyse this by considering a plane wave solution
for the 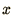 -dependence
by substituting
-dependence
by substituting
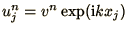 to
obtain
to
obtain
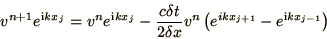 |
(2.15) |
or, after dividing out the common exponential factor,
![\begin{displaymath}
v^{n+1} = \left[ 1 - \i{c\delta t\over\delta x} \sin(k \delta x)
\right]v^n.
\end{displaymath}](img187.png) |
(2.16) |
Since the wave and
advection equations express a
conservation law
the solution should neither grow nor decay as a function
of time. If we substitute
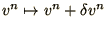 and subtract
(2.16) we obtain an equation for
and subtract
(2.16) we obtain an equation for 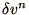
![\begin{displaymath}
\delta v^{n+1} = \left[ 1 - \i{c\delta t\over\delta x} \sin(k \delta x)
\right]\delta v^n
\end{displaymath}](img190.png) |
(2.17) |
which is identical to (2.16).
Hence the stability condition is simply given by the quantity
in square brackets. We call this the
amplification factor and write it as
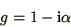 |
(2.18) |
where
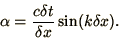 |
(2.19) |
As  is complex the stability condition becomes
is complex the stability condition becomes
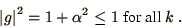 |
(2.20) |
The condition must be fulfilled for all wave vectors 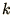 ; otherwise a
component with a particular
; otherwise a
component with a particular 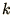 will tend to grow at the expense of the
others. This is known as the
von Neumann stability condition2.2.
Unfortunately it is never fulfilled for the simple method applied to the
advection equation: i.e. the method is unstable for the advection
equation.
will tend to grow at the expense of the
others. This is known as the
von Neumann stability condition2.2.
Unfortunately it is never fulfilled for the simple method applied to the
advection equation: i.e. the method is unstable for the advection
equation.



Next: An Improved Algorithm
Up: Hyperbolic Equations
Previous: Hyperbolic Equations