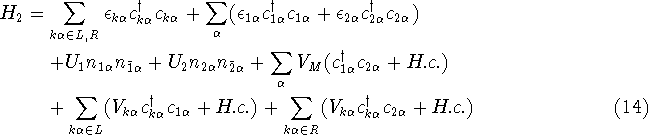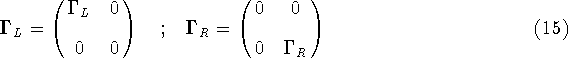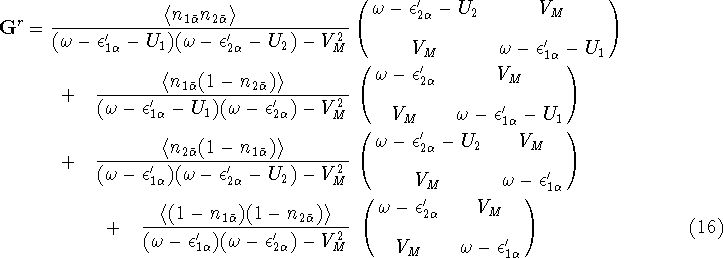The single dot Hamiltonian can easily be extended
to describe two quantum dots in series. As before, assume that there is
only one spin-split level per dot and that the electrons experience an
on-site interaction energy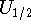 
.
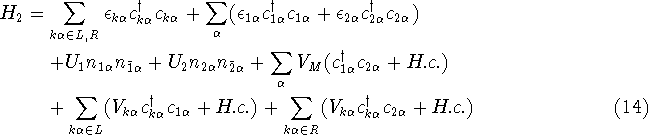
As before the dots are coupled to the reservoirs by the hopping potentials
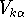, but there is also some coupling 
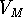between the dots.
In this representation the coupling matrices for each spin are given by
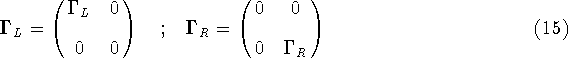
Now that there is more than one dot in the interacting region, it is clear
that the correlations between the occupation numbers of the dots become
important, since the occupation of one dot will depend on the occupation
of the other.
The equivalent of approximation scheme 1 actually ignores this correlation.
Here the approximation scheme 2 will be employed, where the reservoirs are
included in the form of a self-energy.
The single particle Green's function matrix for spin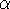 
is given by
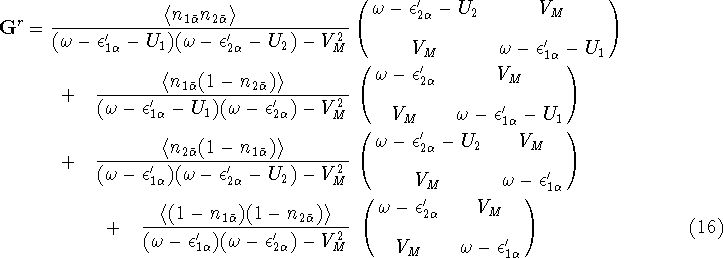
where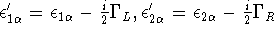 
.
As for the single dot case,
the Green's functions have a straightforward probabilistic interpretation.
They treat the electrons of opposite spin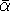 
as static entities
whose main influence is to change the effective site energy of the
electrons of spin 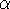by U. Each Green's function is
simply a sum over effective non-interacting Green's functions
each weighted by the probability of a particular realisation of the
occupation numbers for the opposite spin states. Of course the single
particle energy levels have to be
adjusted to correspond to the correct occupations of the opposite spin
states.
This form of the Green's function has some important consequences.
First of all the distribution, retarded and advanced
self-energies can be written in terms of the coupling matrices:
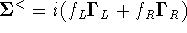and
.
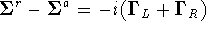Substitution of the equalities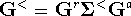 
and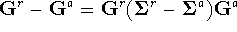 
into equation 4 yields a condensed form of the current formula
for non-interacting systems.
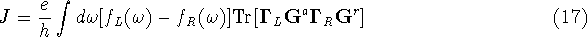
Using equations 15 for the double dot this reduces to
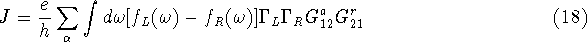
Secondly, the coupling matrices
are no longer proportional, which results in a non-diagonal form of the
distribution matrix at finite bias.
Thirdly, the probabilistic form of the Green's functions
warrants a statistical approach for the multiplication of Green's functions.
Since the Green's functions are probabilistic sums over non-interacting
Green's functions, products of Green's functions must be expressed as
probabilistic sums over the products of the appropriate non-interacting
Green's functions.
Fourthly, higher order Green's functions, needed to
calculate correlations of the type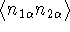 
, can also be
reduced to a sum over non-interacting Green's functions.
For a non-interacting system it can be shown that
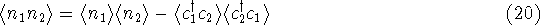
In the presence of interaction on the dots, the correlation 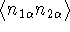is obtained by taking the probabilistic sum over all
possible occupation realisations of the opposite spin states.
Taking the four points above into account, the current and conductance characteristics can be calculated.