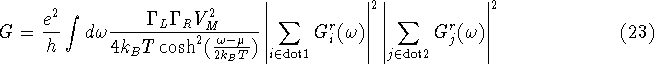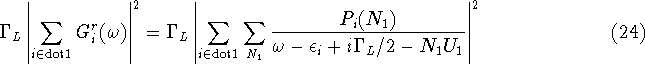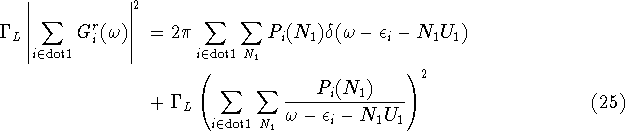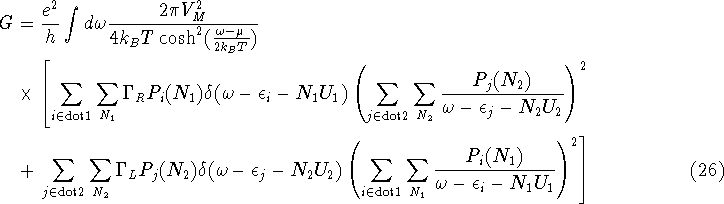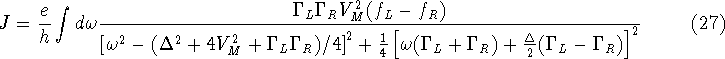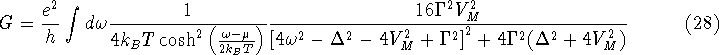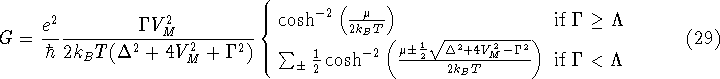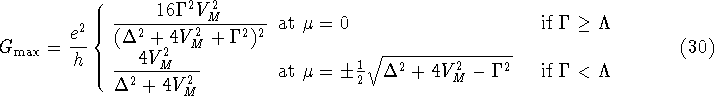Finally, the more realistic case of the Ohmic conductance through a double
dot with an infinite number of energy levels will be calculated. The simple
case of negligible broadening and small inter-dot coupling will be considered.
The coupling to the reservoirs in the 'site' representation is given by
the following matrices:
The matrix is subdivided into four infinite sub-matrices, corresponding to
coupling either between levels of the same dot or between levels of different
dots, e.g. the top left sub-matrix includes all couplings between levels of
the first dot. The sub-matrices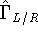 
are defined as a matrices whose
elements are all given by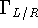 
.
As before the current will be determined using equation 17.
Substitution of the coupling matrices and taking the limit of an infinitesimal
(Ohmic) bias across the system yields the conductance equation.
Analogous to expression 18 the conductance only depends on the
Green's functions between states in different dots.
Treating the inter-dot coupling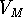 
as a small perturbation allows these
off-diagonal Green's functions to be written as
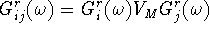so that
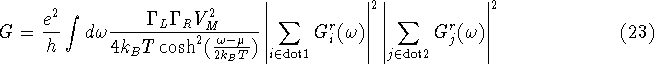
In this approximation the diagonal elements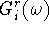 
of the Green's function
are identical to those of the single dot with multiple levels [3]. Hence
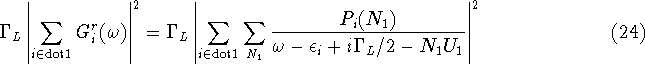
where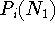 
is the probability that the first dot contains 
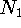electrons
on levels other than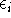 
. In the limit of negligible broadening this
becomes
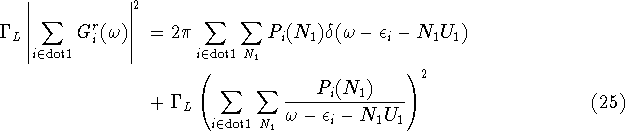
The first part of the expression shows the behaviour at energies coinciding
with an energy level whereas the second part gives the off-resonance
contribution. A similar expression may be obtained for the Green's functions
of the second dot. Note that the limit of small broadening excludes the
possibility of
energy levels in the two dots matching up exactly (this case will be
examined later in more detail), so that the conductance formula 23
can be rewritten as
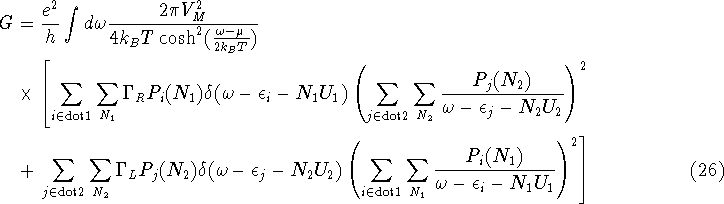
In figure 6 the Ohmic conductance has been plotted for
a system where the dots have a different level spacing and Coulomb interaction.
As expected at low temperatures,
the conductance peaks are largest at values of the chemical potential where the
charge degeneracy points of the two dots are close in energy. At the charge
degeneracy point between the occupations N and N+1 the (N+1)th single
particle level is dominant.
As the temperature is raised there is a higher probability of other levels
contributing to the current. This has
a particularly strong effect when any of the newly available subsidiary levels
very nearly match up (as at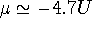 
). Otherwise a rise in
temperature simply causes the peaks to be smeared. At higher temperatures
the periodicity of the smaller dot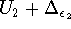 
can easily be estimated
from the spacing of the peaks in the conductance plot.
At this stage it is useful to analyse the height and shape of the
conductance peaks in more detail. Moreover, in order to compare the coherent
case with other tunnelling mechanisms, it would be helpful to obtain an
expression for the current through the double dot at finite bias as a function
of the gate potential of one of the dots.
At low temperatures these quantities can be investigated by just
considering the dominant levels in each of the dots. Their energy
difference is simply the separation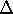 
between the nearest charge degeneracy
points. Since this is now a
non-interacting system, the Green's functions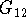 
of the current
formula 18 can be calculated exactly. It is also possible to
include the effect of non-negligible dot-reservoir and inter-dot coupling.
This yields
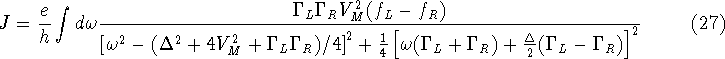
First, consider the peak characteristics of the Ohmic conductance.
This is obtained simply by differentiating with respect to
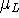and setting 
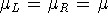. Thus, for 
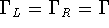, one obtains
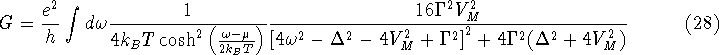
This shows that the conductance is determined by the product of a
thermal broadening factor and a term which is a Lorentzian in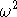 
of
width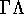 
where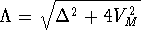 
. Depending on the relative
width of the two terms, two limiting cases will be of relevance.
In the limiting case of small reservoir-dot coupling
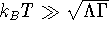the conductance can be rewritten
as
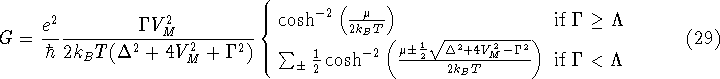
which is clearly consistent with expression 26 for negligible
reservoir-dot and inter-dot coupling. This shows that, as a result of the
level repulsion and the broadening, the
conductance does in fact not diverge at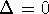 
in this limit. Moreover,
the peak height is inversely proportional to the temperature, as was the
case for the Ohmic conductance through a single dot.
The question whether the conductance diverges at all will now be considered
by taking the opposite limit of vanishing temperature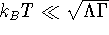 
.
It appears that the conductance either has a single peak or a split peak.
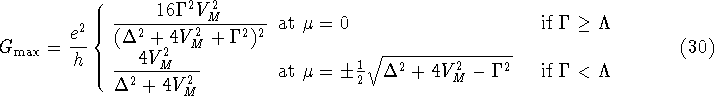
This shows that the conductance will not diverge but has a maximum value
imposed by the conductance quantum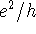 
, which can only be reached
when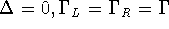 
and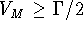 
. For asymmetric tunnelling
barriers to the reservoirs, the conductance is maximised at
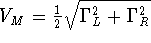and gives a maximum conductance of
.
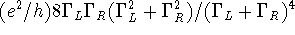Secondly, an expression will be derived describing the current peaks which
occur at finite bias when the gate voltage of one of the dots is raised.
As before, only a single level per dot will be taken into account. Assuming
that the energy window 
is sufficiently large, the integral in
the current equation 27 can be solved analytically by finding
the residues of the poles of the integrand in the Argand plane.
This yields
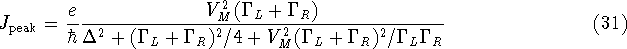
The current peak has a Lorentzian line shape with a width that is at least
as large as the combined width of the single particle levels in the two dots.
This is consistent with the experimentally observed line shape [18].
In the limit of large coupling the same maximum current results as for the
single dot case.