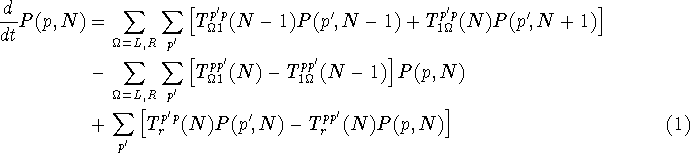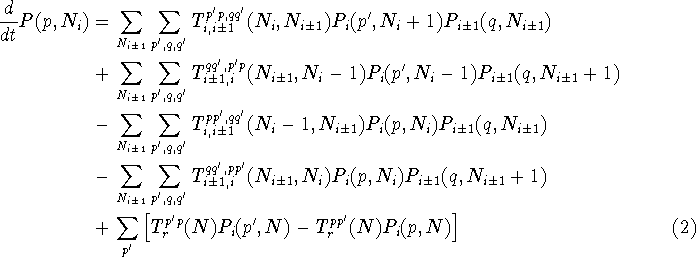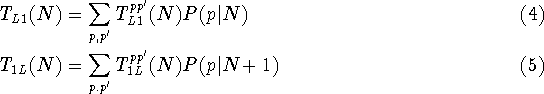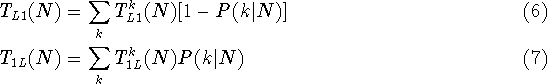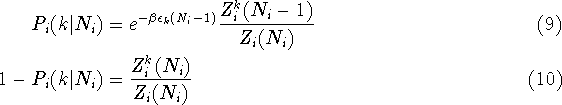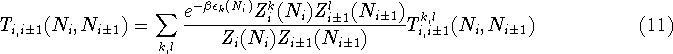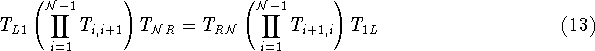Next: The canonical distribution
Up: Incoherent tunnelling through two
Previous: Incoherent tunnelling through two
When it is assumed that the tunnelling rates are small compared to the
Coulomb energy and the average level spacing, then use of the master
equation is justified [13].
In order to take account of the discrete nature of the energy-levels in the
dot, the master equation method for dots with a continuous energy level
spectrum [6]
has to be generalised. The tunnelling rates not only depend on the
number of electrons in the dot, but also on their configuration, i.e. how
the electrons are distributed over the available energy levels. When there is
a high relaxation rate, then the electrons will revert to their local
equilibrium distribution between tunnelling events. This is likely to be the
case for small tunnelling
barriers which cause the electrons to spend a long time in the dot.
Since this distribution will depend only on the temperature,
the state of the dot may yet again be described simply in terms of the
number of electrons present in the dot.
Let P(p,N) be the probability that the system is in a state which is
characterised by N electrons in the dot which are distributed over the
energy levels according to a configuration p.
Define 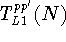 as the tunnelling rate coefficient corresponding
to the transition
as the tunnelling rate coefficient corresponding
to the transition 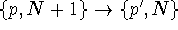 by an electron tunnelling
through the left barrier.
by an electron tunnelling
through the left barrier. 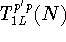 refers to the rate that corresponds
to the reverse process. The tunnelling rates through the right barrier
are defined similarly. Finally, there are the relaxation rates
refers to the rate that corresponds
to the reverse process. The tunnelling rates through the right barrier
are defined similarly. Finally, there are the relaxation rates 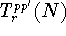 which account for the intra-dot transitions at a fixed electron occupation
N.
The rate of change of the probability of occurrence of the state
which account for the intra-dot transitions at a fixed electron occupation
N.
The rate of change of the probability of occurrence of the state 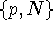 is
thus given by
is
thus given by
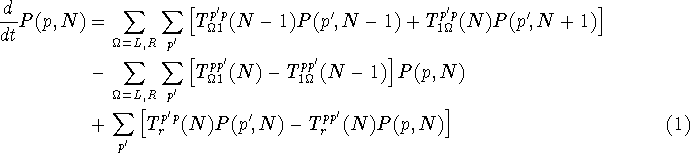
If the system consists of several dots in series, then the above formalism
needs to be extended and it is necessary to
define the tunnelling rates between the dots.
Define 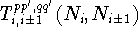 as the tunnelling rate
corresponding to the transition
as the tunnelling rate
corresponding to the transition
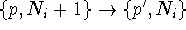 and
and
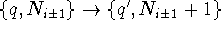 where the subscript i labels the site of the dot.
The evolution of the multi-particle state occupation probabilities
for a dot not neighboured by a reservoir is given by
where the subscript i labels the site of the dot.
The evolution of the multi-particle state occupation probabilities
for a dot not neighboured by a reservoir is given by
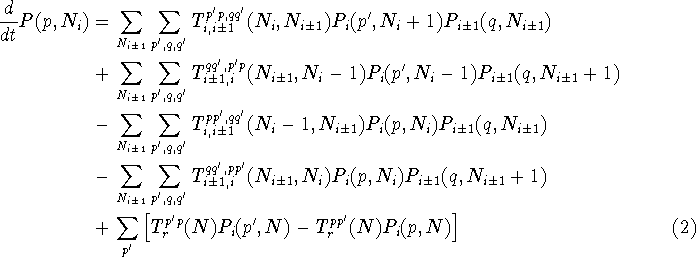
For both the single and the multiple dot system the steady state current can
be written as
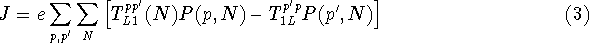
When it is assumed
that the relaxation rates are large compared to the tunnelling rates, then
the number of electrons in the dots is the only significant variable, since
knowledge of this quantity
allows one to deduce the
probabilities of the various electronic configurations. Hence the formalism
is greatly simplified. However, the
tunnelling rates between states with a different occupation number have to be
redefined to include the weighted sum over all possible tunnelling paths.
Define 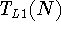 and
and 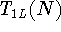 as the tunnelling rates for an electron
tunnelling into and out of the dot through the left barrier with N other
electrons present in the dot.
as the tunnelling rates for an electron
tunnelling into and out of the dot through the left barrier with N other
electrons present in the dot.
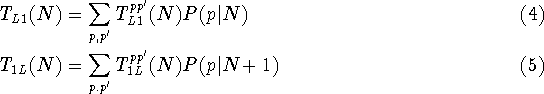
where P(p|N) is the conditional probability that the system is in
configuration p given that there are N electrons in the dot.
Since the master equation takes only single electron tunnelling events into
consideration, the only contributions that need to be taken into account are
those
where p and p' differ by the occupation of one energy level. Therefore
the double sum over p and p' can be replaced by a single sum over the
single particle energy levels k.
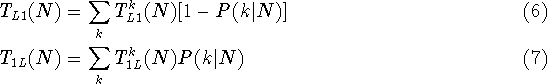
Here P(k|N) is the conditional probability that level k is occupied
given that there are N electrons in the dot.
For inter-dot tunnelling events the rates are re-expressed in terms of a
sum over the tunnelling paths from
all levels k in dot i to all levels l in dot 
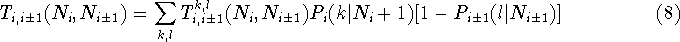
For the case of negligible energy level broadening the probability
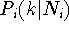 of finding an electron on level k of dot i given
of finding an electron on level k of dot i given 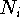 electrons can be determined from the Boltzmann distribution.
electrons can be determined from the Boltzmann distribution.
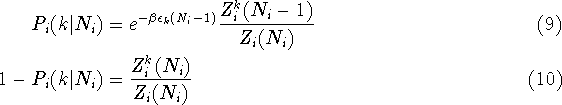
where 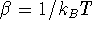 and
and 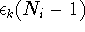 is the energy required to add an electron
at an energy level k when
is the energy required to add an electron
at an energy level k when 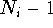 electrons are already present in the dot.
electrons are already present in the dot.
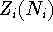 is the partition function for
is the partition function for 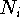 electrons in dot i,
electrons in dot i,
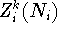 is the conditional partition function for
is the conditional partition function for 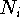 electrons
given that level k is unoccupied.
When the conditional probabilities are substituted in equation 8,
one obtains
electrons
given that level k is unoccupied.
When the conditional probabilities are substituted in equation 8,
one obtains
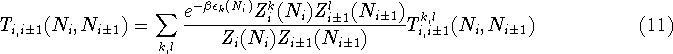
Tunnelling events between dots will in general not preserve energy, since it is
unlikely that energy levels will line up.
The high relaxation rate suggests that all tunnelling events can be
considered inelastic.
Hence
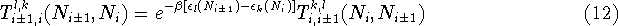
It follows from the two preceding equations that
the tunnelling rates are inelastic in the total free energy of the system.
This is also true for tunnelling between dot and reservoir. This implies that
the following condition holds true at zero bias for 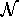 dots for all
possible occupation numbers
dots for all
possible occupation numbers 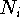 .
.
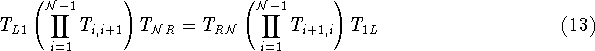



Next: The canonical distribution
Up: Incoherent tunnelling through two
Previous: Incoherent tunnelling through two
Angus MacKinnon - Aonghus Mac Fhionghuin
Fri Nov 8 18:10:54 gmt 1996