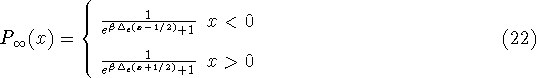One of the quantities that is needed to calculate the tunnelling rate
between dots of specified occupation number is the probability P(k|N) that
an energy level k is occupied given a total occupation of N electrons.
When no relaxation of the electrons in the dot is allowed the occupation of
the levels will be determined by the coupling to the reservoirs. However,
in the presence of thermalisation the levels will be filled according to
some equilibrium distribution independent of the energies at which the
electrons initially entered the dot.
In metals the energy-levels are filled according to the Fermi-Dirac
distribution function. Naively one might expect this also to hold for
discrete energy levels and this has been assumed in various papers.
Unfortunately, this is not generally the case. In metallic
systems the levels are very closely spaced so that the addition of an
additional electron will have no effect on the distribution, whereas
this is not true for a discrete level spectrum.
In this section the correct
distribution will be calculated for a dot with an infinite number of
equally spaced energy levels, containing N electrons. The calculation is
done for energy levels with negligible broadening (
).
Consider the partition function Z(N) for a dot containing N electrons,
with energy levels 
.
where the sum is taken over all realisations 
with 
.
Explicitly expand out the contribution of the lowest energy level
(either 
or 
).
When it is assumed that there is an infinite number of energy levels,
then the sum over the occupation numbers 
(k > 1) can be transformed
to the partition function over all levels (including k=1).
Rewriting 
and relabelling 
,
the following recursion relation is obtained.
With the boundary condition given by Z(0)=1, this is solved to give
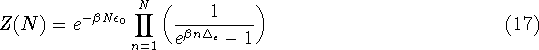
This expression for the partition function does not
explicitly include the many-body
interaction. This
is irrelevant in this context, since the number of electrons is kept
constant. However, when one wants to calculate the
probability that the dot contains a certain number of electrons, the
Coulomb interaction obviously needs to be included. For a
simple model of the interaction where all pairs of electrons have an
associated Coulomb repulsion U, the full interactive partition
function is obtained
by multiplication with a factor 
.
Now it is possible to do a similar calculation to obtain an expression for
, the conditional partition function for N electrons
given that level k is unoccupied.
However, in contrast to the full partition function, this requires
one to solve a recursion relation in both parameters k and N. This can
be avoided by using equations 9 and 10 to yield a
recursion relation of the conditional probability P(k|N) directly.
Since the full partition functions are known, this is easily solved to give
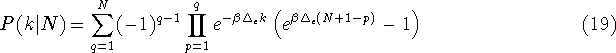
In order to compare this with the Fermi-Dirac distribution function, one
needs to consider a very large number of electrons in the dot. The
occupation probability will depend only on the difference x=k-N-1/2.
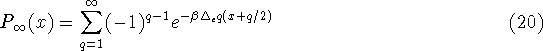
For computational reasons the above equation is rewritten as
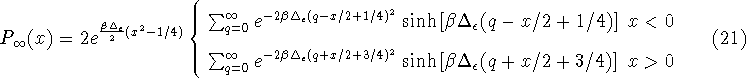
The distribution function has been plotted in figure 1
for various values of 
. In the metallic limit, when the
level spacing is small compared to the temperature, the distribution
tends towards the Fermi-Dirac distribution function, as expected.
When the temperature is comparable or smaller than the
level spacing, the distribution deviates significantly. Its limiting
behaviour is well described by another Fermi-Dirac distribution function
with an effective temperature which is half the real temperature.
A slightly more accurate result for the occupation probability in the
limit 
is given by (note that 
by
definition)
