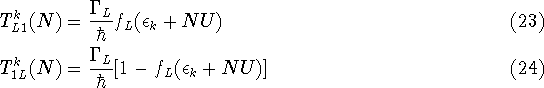
When the energy level broadening is negligible compared to the temperature,
i.e. in the limit of weak coupling to the reservoirs, the density of
states in the dot can be adequately described by a set of delta functions.
The leads are assumed to be in thermal equilibrium, described by the
Fermi-Dirac distributions 
and 
. To a first approximation,
the electron-electron interaction can
satisfactorily be described using the charging model, where each pair of
electrons has an associated Coulomb repulsion of U.
Fermi's golden rule
gives the tunnelling rates between the dot and the reservoirs for all
energy levels k.
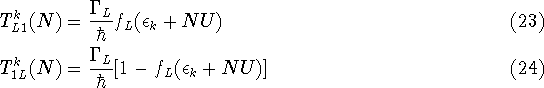
where 
is the strength of coupling to the left
reservoir. The expressions for the tunnelling rates through the right barrier
are similar.
It is assumed that the quantum dot can be approximated by
a parabolic confining potential so that the single particle energy levels
are equally spaced by an energy 
. In figures 2
and 3 the current and its associated differential conductance
is plotted as a function of the applied bias for a range of energy level
spacings.
In numerical calculations it is possible to take into account more
realistic energy level spectra, enabling a closer comparison with
experiment. When it is taken into account that the total spin of the
system can only change by 1/2 with each tunnelling event, it appears
that negative differential conductance may occur in specific regions
[14, 15].
In general a dot with closely packed energy levels yields a higher current
than a dot with a sparse energy level spectrum, because of the higher number of
current paths available. When 
then the metallic
regime is entered.
When the energy level spacing is not negligible, the I-V characteristics are
typified by two energy scales, the Coulomb repulsion energy U and the
bare energy level spacing . As in the metallic regime, one expects
the I-V characteristic to display a current step whenever the maximum
occupation of the dot increases by one. This happens with a period 
,
since an extra electron not only has to overcome the Coulomb barrier but also
has to tunnel to the next available energy level. In addition, there is
also some fine structure which has an associated period of . This is
caused by the fact that an extra current path is created when the bias is
increased by .
When 
the dot will be mostly maximally occupied and the most
marked current increases occur whenever the Coulomb blockade can be overcome.
This means that the period is accentuated.
In the opposite regime 
the dominant period is the level
spacing.
Under normal operating conditions 
the two periods coexist
(see figure 3). It is noted that at higher bias voltages the
number of peaks in the differential conductance increases, as new current
paths become available at different energies for different occupation numbers.
Only when the ratio 
is an integer do peaks corresponding to
different occupation numbers coincide.
The Ohmic conductance through a quantum dot (figure 4) differs
from that through a metallic dot in two
significant ways. Firstly, the periodicity of the conductance peaks has
increased by the level spacing . Secondly, the temperature
dependence of the peaks has changed its nature. An increase in temperature
now not only leads to larger thermal broadening, but also to a lowering of
the peak amplitude which is inversely proportional to the temperature.
This is due to the fact that transport proceeds through
a single energy level. The temperature dependence is proportional to the
derivative of the Fermi-distribution function in the reservoirs [16].
Therefore,
at low temperatures 
the Ohmic conductance can be written as
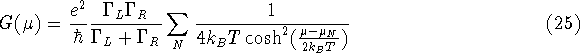
where the successive charge degeneracy points 
are spaced by an energy
. For higher temperatures several levels should be taken into
consideration, each of which is weighted by a factor determined by the
Boltzmann distribution [10].
where 
is the joint probability that the dot contains N electrons and
that the single particle level 
is empty.
Note that the contributions from levels other than at positions
are too small to cause a peak in the conductance.
Apart from the I-V characteristics and the Ohmic conductance, there is a
third useful experiment that can be carried out. This involves applying a
constant bias across the dot and studying the resultant current as a function
of the gate potential. Typically the source-drain bias is chosen to be
less than the charging energy which isolates the effects of the
energy separation of the zero dimensional states of the dot. In figure
5 the current has been calculated as a function of the
gate voltage for a dot with a constant level spacing 
. The
thermal energy is given by 
.
In accordance with some recent experiments [17, 18, 19]
a number of peaks and troughs can be observed in the current. All peaks
and troughs can be characterised by the number of levels available to an
incoming electron to tunnel onto, and the number of levels from which an
electron can tunnel out of the dot. For a Fermi level separation 
of 0.15 U between the reservoirs (see figure 5)
these numbers are
. This explains why the total peak
is split into two subpeaks. For the second set of graphs with 
the sequence of
available tunnelling levels is 
. It is also clear that asymmetric tunnelling barriers
cause the current peaks to be asymmetric.