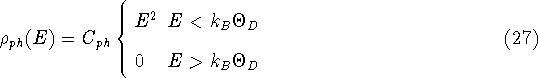
In a two-dimensional electron gas the Debye temperature
When studying the current and conductance properties of two quantum dots connected in series between the source and the drain, one obviously has to take into account the tunnelling between the dots. Inter-dot transitions are qualitatively different from transitions between a dot and a reservoir. The reservoir can be assumed to have a continuous density of states, so that electrons can always tunnel elastically into and out of the reservoir. Even though inelastic tunnelling events would in principle be allowed, their contribution would be relatively small compared to the elastic tunnelling rate. Therefore inelastic scattering only has a significant effect on the transport through a single dot if the scattering takes place inside the dot, i.e. relaxation.
As far as tunnelling between dots is concerned, it is clear that the elastic tunnelling rate is significant only when the energy levels in the dots line up. This is obviously not generally the case. Usually an electron would have to interact inelastically in order to tunnel to a different energy level in the neighbouring dot. The energy difference would normally be absorbed or provided by phonons.
As a theoretical model, one can consider the double dot system to be
coupled to a phonon reservoir or a heat bath with a coupling strength
![]() . The energy spectrum of the independent oscillators of the
phonon reservoir is characterised by the density of phonon states
. The energy spectrum of the independent oscillators of the
phonon reservoir is characterised by the density of phonon states
![]() . Some work has been done
to calculate the current through a double-barrier resonant structure with
some interaction between electrons and photons [20, 21, 22].
The coupling to the optical phonons creates transmission subbands which are
observable in the I-V characteristics.
In this section, where inter-dot transmission is considered, the interaction
with acoustic phonons will be the dominant mechanism. The energy spectrum
for acoustic phonons is given by the Debye density of states.
. Some work has been done
to calculate the current through a double-barrier resonant structure with
some interaction between electrons and photons [20, 21, 22].
The coupling to the optical phonons creates transmission subbands which are
observable in the I-V characteristics.
In this section, where inter-dot transmission is considered, the interaction
with acoustic phonons will be the dominant mechanism. The energy spectrum
for acoustic phonons is given by the Debye density of states.
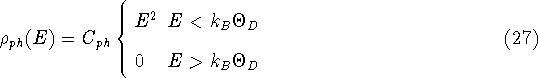
In a two-dimensional electron gas the Debye temperature ![]() is
approximately in the range
is
approximately in the range ![]() [23]. This
is of the order of a few tens of meV, which corresponds to several
times the Coulomb interaction energy U. This is typically larger than
the voltage drop across the device, so that one can simply use the
phonon density of states below the cut-off energy
[23]. This
is of the order of a few tens of meV, which corresponds to several
times the Coulomb interaction energy U. This is typically larger than
the voltage drop across the device, so that one can simply use the
phonon density of states below the cut-off energy ![]() .
.
Phonons are bosons, so that the Pauli principle does not apply
and states can be multiply occupied. The average occupation number of
states at a given energy is given by the Bose-Einstein distribution
![]() .
.
![]()
where ![]() is the Heaviside step function and E(-E) is the
energy provided (absorbed) by the phonon bath. The Bose-Einstein
distribution at positive and negative values of E differs by 1, which
is indicative of the fact that a heat bath can always absorb energy.
is the Heaviside step function and E(-E) is the
energy provided (absorbed) by the phonon bath. The Bose-Einstein
distribution at positive and negative values of E differs by 1, which
is indicative of the fact that a heat bath can always absorb energy.
Any plausible model for the inelastic tunnelling rate between the dots
should take into account a Boltzmann factor,
the density of states in the two dots and a term which describes the
hybridisation between levels in adjacent dots.
A simple model for the inelastic tunnelling rate ![]() between an
energy level
between an
energy level ![]() in the first dot and
in the first dot and ![]() in the second dot is
as follows
in the second dot is
as follows
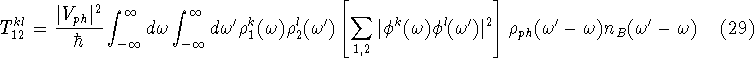
where ![]() and
and ![]() are the densities of state for the
energy levels. Considering the dots in isolation from the reservoirs, the
eigenstates cannot be regarded as localised in each of the dots, but the
wavefunctions will leak slightly into the other dot by virtue of the
hopping potential
are the densities of state for the
energy levels. Considering the dots in isolation from the reservoirs, the
eigenstates cannot be regarded as localised in each of the dots, but the
wavefunctions will leak slightly into the other dot by virtue of the
hopping potential ![]() . This results in the overlap integrals
. This results in the overlap integrals
![]() and
and
![]() . Naively this can be
interpreted as the probability that the inelastic process can take place
between the wavefunction components in the same dot. If a specific
system is studied, then it is required to investigate the energy dependence
of the off-diagonal elements of the Hamiltonian. However, here we are mostly
concerned with generic features, so that
the wavefunctions are calculated from a
simple two-dimensional Hamiltonian with diagonal elements
. Naively this can be
interpreted as the probability that the inelastic process can take place
between the wavefunction components in the same dot. If a specific
system is studied, then it is required to investigate the energy dependence
of the off-diagonal elements of the Hamiltonian. However, here we are mostly
concerned with generic features, so that
the wavefunctions are calculated from a
simple two-dimensional Hamiltonian with diagonal elements ![]() and
and ![]() and
off-diagonal elements given by the constant hopping potential
and
off-diagonal elements given by the constant hopping potential ![]() .
By calculating its eigenvectors the overlap matrix can be determined.
.
By calculating its eigenvectors the overlap matrix can be determined.
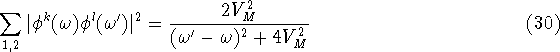
The above model is chosen for its relative simplicity, but it is expected
to give results which are at least qualitatively correct. In principle, it is
also possible to use this method using a more sophisticated model for the
interdot tunnelling rate.
The density of states in the dots is broadened mainly as a result of the
inelastic scattering, which is a prerequisite for the incoherent regime.
To a first approximation the broadening can be considered as a Lorentzian
distribution [24] with a broadening ![]() proportional to the phase-breaking rate. Now equation 29 can
be rewritten as a single integral over the energy difference
proportional to the phase-breaking rate. Now equation 29 can
be rewritten as a single integral over the energy difference ![]() between the initial and final state.
between the initial and final state.
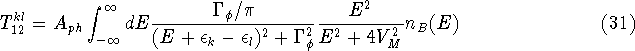
with ![]() .
.
It must be stressed that the broadening of the energy levels should be
much less than the temperature. Otherwise it is not valid anymore to
use the Boltzmann distribution to calculate the occupation probabilities.
This assumption is consistent with the calculation of the reservoir-dot
transition
rate of section iii. Figure 6a shows the
energy dependence of the inter-dot tunnelling rate for the case
when the energy-levels are considered
to be ![]() -functions. However, it should still be taken into account
that the level broadening is large compared to the coupling between the
dots, causing the peaks in the transition rate at
-functions. However, it should still be taken into account
that the level broadening is large compared to the coupling between the
dots, causing the peaks in the transition rate at ![]() to be
smeared. At energy differences
to be
smeared. At energy differences ![]() which are small
compared to the broadening, the transition rate can now be approximated by
a Lorentzian of width
which are small
compared to the broadening, the transition rate can now be approximated by
a Lorentzian of width ![]() and height
and height
![]() (see figure 6b).
At larger energy differences
(see figure 6b).
At larger energy differences ![]() the
function is sufficiently close to the Bose-Einstein distribution.
the
function is sufficiently close to the Bose-Einstein distribution.
As the broadening is much smaller than the thermal energy, the inter-dot
transition rate for small ![]() can get much larger than the transition rate between dot
and reservoir so that the inter-dot transition is no longer the
current-limiting process. In this case it is of no relevance whether the
transition rate between the dots is infinite or simply very large.
This suggests that the inter-dot transition rate may be approximated by
the Bose-Einstein distribution
can get much larger than the transition rate between dot
and reservoir so that the inter-dot transition is no longer the
current-limiting process. In this case it is of no relevance whether the
transition rate between the dots is infinite or simply very large.
This suggests that the inter-dot transition rate may be approximated by
the Bose-Einstein distribution ![]() at all values of
at all values of ![]() .
This makes the mathematical analysis much more transparent.
.
This makes the mathematical analysis much more transparent.
When one calculates the transition rate between dots with a given occupation
number, one should sum over all possible tunnelling events according to
equation 8. The greatest contribution should come from the energy
range where the electron can tunnel from levels which are mostly
occupied to levels which are mostly empty. Outside this window
the product ![]() falls off exponentially.
However, since the Bose-Einstein distribution diverges at
falls off exponentially.
However, since the Bose-Einstein distribution diverges at ![]() , the total transition rate seems to be dominated by matching levels,
even when they are situated at energies far removed from the Fermi level.
This is clearly an unphysical situation. This anomaly can be removed
by again including the broadening in the calculation of the transition rate.
Alternatively, it can be argued that the transition rate for a given pair
of levels is the combination of the previously defined rate and the
rate at which electrons can get into an excited level. This second rate is the
relaxation rate
, the total transition rate seems to be dominated by matching levels,
even when they are situated at energies far removed from the Fermi level.
This is clearly an unphysical situation. This anomaly can be removed
by again including the broadening in the calculation of the transition rate.
Alternatively, it can be argued that the transition rate for a given pair
of levels is the combination of the previously defined rate and the
rate at which electrons can get into an excited level. This second rate is the
relaxation rate ![]() . Remembering that the inverses of
the rates of consecutive processes add together, the total inter-dot rate
can be obtained for given occupation numbers.
. Remembering that the inverses of
the rates of consecutive processes add together, the total inter-dot rate
can be obtained for given occupation numbers.
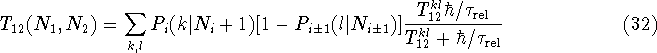
In order to perform some realistic simulations it is helpful
to know the dependence on the size of both the charging energy U and the
confinement energy ![]() . In the charging model approximation the
Coulomb repulsion is inversely proportional to the capacitance C of the dot.
This implies that the repulsion energy U is also inversely proportional to
the area of the dot. The single particle energy level spacing is given by
[25]
. In the charging model approximation the
Coulomb repulsion is inversely proportional to the capacitance C of the dot.
This implies that the repulsion energy U is also inversely proportional to
the area of the dot. The single particle energy level spacing is given by
[25]
![]()
where ![]() is the effective mass of an electron in the two dimensional
electron gas in which the quantum dot has been defined. It follows that
both the Coulomb energy and the level spacing scale inversely proportionally
to the area of the quantum dot.
is the effective mass of an electron in the two dimensional
electron gas in which the quantum dot has been defined. It follows that
both the Coulomb energy and the level spacing scale inversely proportionally
to the area of the quantum dot.