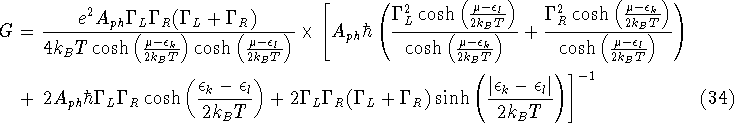
When the two reservoirs are equally strongly coupled to the dots, i.e.
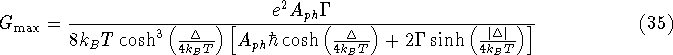
When the peak height is investigated as a function of the temperature, then it appears that it has a maximum at a value of
Figure 7 shows the Ohmic conductance through two dots with
a relatively strong inelastic tunnelling coefficient ![]() .
In order to analyse the structure of the peaks, assume that the total
occupancy of each dot can only fluctuate by one electron. Moreover, assume that
only a single level per dot (at the charge degeneracy points) contributes
substantially to the transport.
Then the global master equation
is used to obtain an expression for the Ohmic conductance.
.
In order to analyse the structure of the peaks, assume that the total
occupancy of each dot can only fluctuate by one electron. Moreover, assume that
only a single level per dot (at the charge degeneracy points) contributes
substantially to the transport.
Then the global master equation
is used to obtain an expression for the Ohmic conductance.
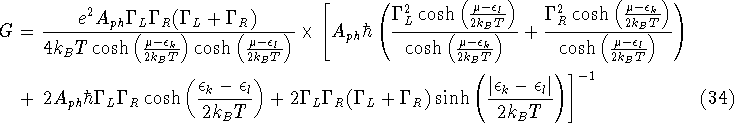
When the two reservoirs are equally strongly coupled to the dots, i.e.
![]() , then the above expression peaks at
, then the above expression peaks at ![]() . The peak conductance is given by (using
. The peak conductance is given by (using ![]() )
)
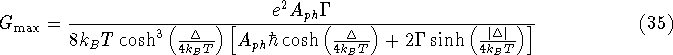
When the peak height is investigated as a function of the
temperature, then it appears that it has a maximum at a value of
![]() which is given by the solution of the following
transcendental equation.
which is given by the solution of the following
transcendental equation.
![]()
The solution is plotted in figure 8. When the ratio
of the inelastic tunnelling coefficient to the reservoir coupling
![]() is of order unity or larger, then the temperature at
which a particular conductance peak reaches its maximum height is given by
roughly half the energy difference
is of order unity or larger, then the temperature at
which a particular conductance peak reaches its maximum height is given by
roughly half the energy difference ![]() . This maximum height is
larger as the energy difference
. This maximum height is
larger as the energy difference ![]() gets smaller.
This calculation is in good quantitative agreement with
the temperature dependence of the
conductance curves of figure 7. At higher temperatures
the calculation becomes more inaccurate as several levels and more
occupation numbers will start to contribute to the transport.
gets smaller.
This calculation is in good quantitative agreement with
the temperature dependence of the
conductance curves of figure 7. At higher temperatures
the calculation becomes more inaccurate as several levels and more
occupation numbers will start to contribute to the transport.
In figure 9 the conductance is shown for a double dot system
which is identical to that of figure 7 with the exception that
the inelastic tunnelling coefficient is two orders of magnitude smaller.
From figure 8 one would expect the peaks to be maximised at
a temperature ![]() . The above description of the
conductance peaks seems to apply to most of the peaks. However, it is clear
that the peak which is situated at
. The above description of the
conductance peaks seems to apply to most of the peaks. However, it is clear
that the peak which is situated at ![]() has an anomalous
behaviour. The conductance at this point is much larger than expected.
This is due to the fact that one of the lower levels in the first dot
very nearly matches up with the dominant level in the second dot, thus
strongly enhancing the inter-dot tunnelling rate.
has an anomalous
behaviour. The conductance at this point is much larger than expected.
This is due to the fact that one of the lower levels in the first dot
very nearly matches up with the dominant level in the second dot, thus
strongly enhancing the inter-dot tunnelling rate.
This effect most strongly shows up when the inelastic tunnelling coefficient
![]() is small compared to the coupling
is small compared to the coupling ![]() to the reservoirs.
This is simply due to the fact that the inter-dot tunnelling is the main
current-limiting process and will therefore tend to dominate the physics.
For large inelastic tunnelling coefficients the current will mainly be
determined by the matching of the levels between dot and reservoir. This
explains why the afore-mentioned effect is almost imperceptible in figure
7.
to the reservoirs.
This is simply due to the fact that the inter-dot tunnelling is the main
current-limiting process and will therefore tend to dominate the physics.
For large inelastic tunnelling coefficients the current will mainly be
determined by the matching of the levels between dot and reservoir. This
explains why the afore-mentioned effect is almost imperceptible in figure
7.