The Influence of Islands



Next: Real wires with
Up: Conductance and conductance fluctuations
Previous: The Influence of
The effects of the strong scattering centers (i.e. islands) in the bulk of the
quantum wire are examined for the case of an otherwise perfect wire with
islands for the system geometry shown in Fig. 6.
As in the case of rough boundaries we consider the conductance of individual
samples as well as the average conductance as a function of energy or wire
length.
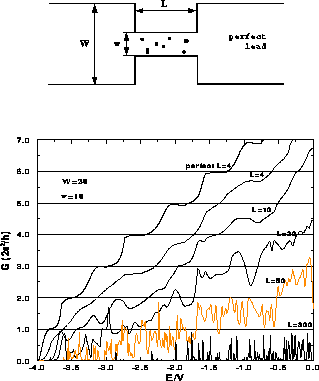
Figure 6: 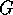 as a function of energy for a single sample of perfect
quantum wire
(width
as a function of energy for a single sample of perfect
quantum wire
(width 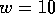 ) with island disorder, for different wire lengths:
) with island disorder, for different wire lengths: 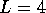 ,
,
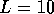 ,
, 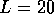 ,
, 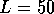 and
and 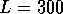 . Island concentration is
. Island concentration is 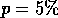 .
Also is presented conductance for
perfect constriction of length
.
Also is presented conductance for
perfect constriction of length 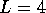 and width
and width 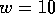 .
The top figure shows the geometry of the system.
.
The top figure shows the geometry of the system.
The conductance of a single sample of a quantum wire with islands is shown in
Fig. 6. Even a small concentration of islands causes an almost
complete suppression of the conductance quantization. In Fig. 6 one
can compare the results for a quantum wire of length 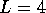 with island
concentration
with island
concentration 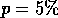 (which means only two islands at random positions) with
the conductance for a perfect wire of length
(which means only two islands at random positions) with
the conductance for a perfect wire of length 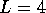 . Island disorder reduces
the conductance in a similar way in each subband. In the mesoscopic regime,
where
. Island disorder reduces
the conductance in a similar way in each subband. In the mesoscopic regime,
where 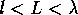 (examples
(examples 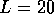 and
and 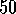 in Fig. 6), the
conductance fluctuates as a function of energy. These fluctuations are of the
order
in Fig. 6), the
conductance fluctuates as a function of energy. These fluctuations are of the
order 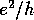 . This is a quantum interference effect in which the scale of the
sensitivity to changes in the energy depends on the length of the wire.
We estimate that this dependence is of the form
. This is a quantum interference effect in which the scale of the
sensitivity to changes in the energy depends on the length of the wire.
We estimate that this dependence is of the form 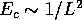 , i.e. similar to
UCF, and differs from that of the fluctuations in the quantum wire with
rough boundaries.
, i.e. similar to
UCF, and differs from that of the fluctuations in the quantum wire with
rough boundaries.
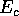 is the change of the Fermi energy
needed to modify the relevant phase differences across the sample by about
is the change of the Fermi energy
needed to modify the relevant phase differences across the sample by about
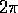 . The fluctuation of the conductance between different samples is also
of order
. The fluctuation of the conductance between different samples is also
of order 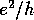 . In the strong localization regime (e.g. case
. In the strong localization regime (e.g. case 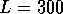 in
Fig.6) the conductance is reduced to a set of peaks of maximum
amplitude
in
Fig.6) the conductance is reduced to a set of peaks of maximum
amplitude 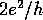 . Each peak corresponds to the occurrence of resonant
tunnelling through the wire. The localization length generally increases as
energy grows and therefore the peaks get higher towards the center of the band.
. Each peak corresponds to the occurrence of resonant
tunnelling through the wire. The localization length generally increases as
energy grows and therefore the peaks get higher towards the center of the band.
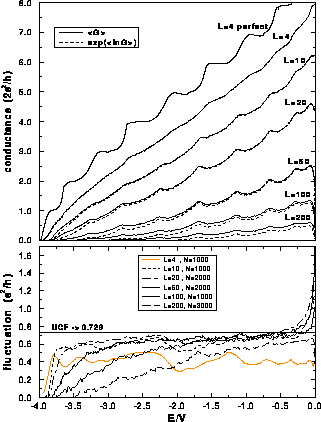
Figure 7: Energy dependence of the average conductance and
conductance fluctuations of perfect wire with islands. Wire lengths are:
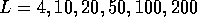 . Island concentration is
. Island concentration is 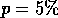 ,
, 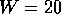 and wire
width is
and wire
width is 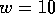 . Number of samples
taken for calculating average values is N. The universal value for UCF of
quasi-1D metallic wires is marked by a horizontal line.
. Number of samples
taken for calculating average values is N. The universal value for UCF of
quasi-1D metallic wires is marked by a horizontal line.
The average conductance for the case of bulk (island) disorder is shown in
Fig. 7 and Fig. 9. This type of disorder has a
similar effect on each subband, unlike the case of edge roughness where higher
subbands are more affected then lower ones. The average conductance as a
function of energy exhibits local maxima near the energies of the subband edges
of the perfect wire (Figures 7 and 8). This
becomes more obvious for the smaller concentrations of islands (e.g. the island
concentrations are 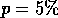 in the case presented in Fig. 7 and
in the case presented in Fig. 7 and
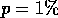 in Fig. 8).
in Fig. 8).
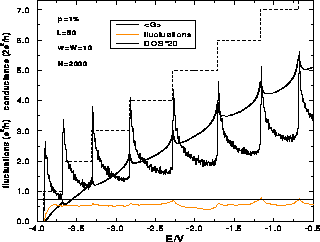
Figure 8: 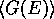 and
and 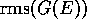 for a perfect wire
with island concentration
for a perfect wire
with island concentration 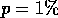 . Steps represent the conductance for the
case of perfect wire. (Note the different units for
. Steps represent the conductance for the
case of perfect wire. (Note the different units for 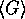 and fluctuations.) The histogram of the (rescaled) DOS for this wire is also
shown.
and fluctuations.) The histogram of the (rescaled) DOS for this wire is also
shown.
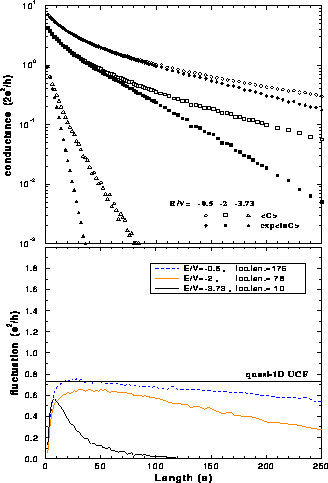
Figure 9: Average conductance as a function of wire length for perfect wire
with islands (concentration 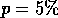 ) for energies
) for energies 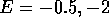 and
and 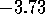 -
upper figure. The corresponding conductance fluctuations are shown in the
lower figure. Number of samples is
-
upper figure. The corresponding conductance fluctuations are shown in the
lower figure. Number of samples is 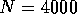 ,
, 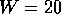 and
and 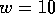 .
.
The behavior of the average conductance of a disordered quantum wire modelled
by the (Anderson) Hamiltonian with a uniform distribution for the site energies
of the wire (Masek and Kramer 1989) is, to some extent, similar. Although the general
appearance of the curves differs (for the strong-scattering regime it looks
like a line with peaks, whereas for the Anderson model it looks like a line
with dips), in both cases the DOS is connected to 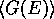 in the same
way. Electron scattering is proportional to the number of available states
into which an electron can be scattered, i.e. to the DOS. Therefore the electron
mobility and conductance should decrease when the DOS increases and vice versa,
see Fig. 8.
in the same
way. Electron scattering is proportional to the number of available states
into which an electron can be scattered, i.e. to the DOS. Therefore the electron
mobility and conductance should decrease when the DOS increases and vice versa,
see Fig. 8.
The average conductance decreases exponentially with the length of the wire,
see Fig. 9, which is the expected behavior for the localized
states. The slope of the line 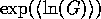 for long wires
determines the localization length for any energy, as defined by the
Eq. (18).
for long wires
determines the localization length for any energy, as defined by the
Eq. (18).
The conductance fluctuations first increase in the quasi-ballistic regime
(Fig. 9), go through a maximum in the region 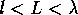 and
then decrease as the length of the wire increases. The decrease is slower for
energies with longer localization lengths. A short region of lengths, where
fluctuations are almost independent of the wire length, can be observed for the
energies
and
then decrease as the length of the wire increases. The decrease is slower for
energies with longer localization lengths. A short region of lengths, where
fluctuations are almost independent of the wire length, can be observed for the
energies 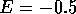 and
and 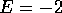 . The level of the fluctuations in this universal
region depends on energy and it is not, in general, equal to UCF value for
quasi-1D metallic systems. However, by chance we have found a case (that is
. The level of the fluctuations in this universal
region depends on energy and it is not, in general, equal to UCF value for
quasi-1D metallic systems. However, by chance we have found a case (that is
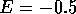 in Fig. 9) where
in Fig. 9) where 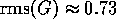 . The
conductance fluctuations (Fig. 7) increase with the energy and
tend to a sort of asymptotical value. This value is close to the UCF constant
for wires with lengths inside the region
. The
conductance fluctuations (Fig. 7) increase with the energy and
tend to a sort of asymptotical value. This value is close to the UCF constant
for wires with lengths inside the region 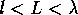 , and decreases as the
wire lengths move out of this region.
, and decreases as the
wire lengths move out of this region.



Next: Real wires with
Up: Conductance and conductance fluctuations
Previous: The Influence of
Angus MacKinnon
Fri Nov 18 13:59:27 gmt 1994

 as a function of energy for a single sample of perfect
quantum wire
(width
as a function of energy for a single sample of perfect
quantum wire
(width 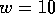 ) with island disorder, for different wire lengths:
) with island disorder, for different wire lengths: 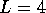 ,
,
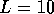 ,
, 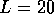 ,
, 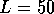 and
and 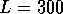 . Island concentration is
. Island concentration is 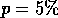 .
Also is presented conductance for
perfect constriction of length
.
Also is presented conductance for
perfect constriction of length 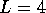 and width
and width 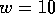 .
The top figure shows the geometry of the system.
.
The top figure shows the geometry of the system.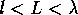 (examples
(examples 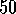 in Fig.
in Fig. 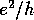 . This is a quantum interference effect in which the scale of the
sensitivity to changes in the energy depends on the length of the wire.
We estimate that this dependence is of the form
. This is a quantum interference effect in which the scale of the
sensitivity to changes in the energy depends on the length of the wire.
We estimate that this dependence is of the form 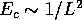 , i.e. similar to
UCF, and differs from that of the fluctuations in the quantum wire with
, i.e. similar to
UCF, and differs from that of the fluctuations in the quantum wire with
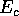 is the change of the Fermi energy
needed to modify the relevant phase differences across the sample by about
is the change of the Fermi energy
needed to modify the relevant phase differences across the sample by about
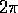 . The fluctuation of the conductance between different samples is also
of order
. The fluctuation of the conductance between different samples is also
of order 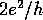 . Each peak corresponds to the occurrence of resonant
tunnelling through the wire. The localization length generally increases as
energy grows and therefore the peaks get higher towards the center of the band.
. Each peak corresponds to the occurrence of resonant
tunnelling through the wire. The localization length generally increases as
energy grows and therefore the peaks get higher towards the center of the band.

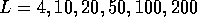 . Island concentration is
. Island concentration is 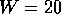 and wire
width is
and wire
width is 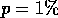 in Fig.
in Fig. 
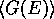 and
and 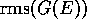 for a perfect wire
with island concentration
for a perfect wire
with island concentration 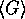 and fluctuations.) The histogram of the (rescaled) DOS for this wire is also
shown.
and fluctuations.) The histogram of the (rescaled) DOS for this wire is also
shown.
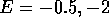 and
and 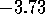 -
upper figure. The corresponding conductance fluctuations are shown in the
lower figure. Number of samples is
-
upper figure. The corresponding conductance fluctuations are shown in the
lower figure. Number of samples is 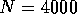 ,
, 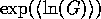 for long wires
determines the localization length for any energy, as defined by the
Eq. (
for long wires
determines the localization length for any energy, as defined by the
Eq. (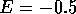 and
and 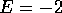 . The level of the fluctuations in this universal
region depends on energy and it is not, in general, equal to UCF value for
quasi-1D metallic systems. However, by chance we have found a case (that is
. The level of the fluctuations in this universal
region depends on energy and it is not, in general, equal to UCF value for
quasi-1D metallic systems. However, by chance we have found a case (that is
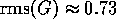 . The
conductance fluctuations (Fig.
. The
conductance fluctuations (Fig.