The Influence of Boundary Roughness



Next: The Influence of
Up: Conductance and conductance fluctuations
Previous: Model and Methods
For the investigation of the transport properties of quantum wires with
rough edges we use the geometry of the system which is shown
at the top of Fig. 2.
The average value of the width is taken to be 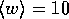 and the
width of the leads will be fixed at
and the
width of the leads will be fixed at 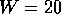 throughout this section.
Here we shall analyse results for four types of calculation:
conductance of a single quantum wire and ensemble average quantities related
to the conductance, as functions of Fermi energy
throughout this section.
Here we shall analyse results for four types of calculation:
conductance of a single quantum wire and ensemble average quantities related
to the conductance, as functions of Fermi energy 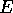 and wire length
and wire length 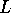 .
Firstly, we discuss the results for the conductance of a single quantum wire
sample, presented in Fig. 2.
.
Firstly, we discuss the results for the conductance of a single quantum wire
sample, presented in Fig. 2.
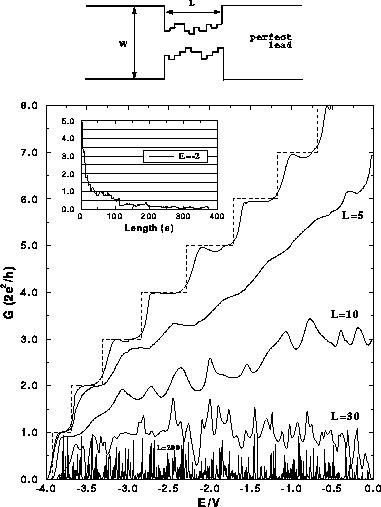
Figure 2: 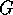 as a function of energy of a single sample of quantum wire
with rough edges and no island disorder, for wire lengths:
as a function of energy of a single sample of quantum wire
with rough edges and no island disorder, for wire lengths: 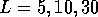 and
and 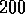 , and average wire width
, and average wire width 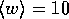 and leads width
and leads width 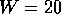 .
Reference step functions are the conductances of the perfect wire of the
width
.
Reference step functions are the conductances of the perfect wire of the
width 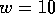 , length
, length 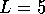 , and leads with
, and leads with 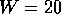 (full line), and
(full line), and 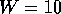 (i.e. no difference between leads and wire - broken line). The
inset is the conductance of a quantum wire
sample as a function of the wire length. The top picture shows the
geometry of the lead-wire-lead system used in the calculations.
(i.e. no difference between leads and wire - broken line). The
inset is the conductance of a quantum wire
sample as a function of the wire length. The top picture shows the
geometry of the lead-wire-lead system used in the calculations.
The edge roughness destroys the conductance quantization steps, firstly near
the band
center for very small disorder (see case 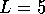 in Fig. 2). The
deterioration of the quantization spreads towards the band edge both as the
disorder and as the length of the wire is increased. In the mesoscopic regime,
when
in Fig. 2). The
deterioration of the quantization spreads towards the band edge both as the
disorder and as the length of the wire is increased. In the mesoscopic regime,
when 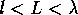 , the conductance
curve shows sample specific fluctuations as a function of energy and length.
However, the
amplitude of these fluctuations is of order
, the conductance
curve shows sample specific fluctuations as a function of energy and length.
However, the
amplitude of these fluctuations is of order 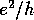 , independent of energy
(Fig. 2,
L=10, L=30) or length (see inset of Fig. 2). This is a quantum
interference effect similar to the universal conductance fluctuations observed
in the mesoscopic regime (Lee and Stone 1985)) of other systems.
The particular value for the conductance is determined by the electron
wavelength (i.e. electron energy), the length of the quantum wire and the actual
realization of the disorder in a
sample. The conditions for the destructive or constructive interference of an
electron wavefront are, generally, very sensitive to all of these parameters.
The scale of the sensitivity to energy, however, differs with the length of the
wire (which is evident from Fig. 2 for
, independent of energy
(Fig. 2,
L=10, L=30) or length (see inset of Fig. 2). This is a quantum
interference effect similar to the universal conductance fluctuations observed
in the mesoscopic regime (Lee and Stone 1985)) of other systems.
The particular value for the conductance is determined by the electron
wavelength (i.e. electron energy), the length of the quantum wire and the actual
realization of the disorder in a
sample. The conditions for the destructive or constructive interference of an
electron wavefront are, generally, very sensitive to all of these parameters.
The scale of the sensitivity to energy, however, differs with the length of the
wire (which is evident from Fig. 2 for 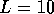 and
and 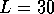 ) or with
the level of disorder. This observation supports the idea that the
fluctuations do not arise from classical scattering from the rough boundary
but from the phase modulation of the electron wavefunction due to multiple
elastic
scattering in the wire (Takagaki and Ferry 1992). We estimate that the typical
spacing between peaks and valleys in the conductance as a function of energy
depends on the wire length as:
) or with
the level of disorder. This observation supports the idea that the
fluctuations do not arise from classical scattering from the rough boundary
but from the phase modulation of the electron wavefunction due to multiple
elastic
scattering in the wire (Takagaki and Ferry 1992). We estimate that the typical
spacing between peaks and valleys in the conductance as a function of energy
depends on the wire length as: 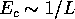 . This is a weaker dependence on
the
wire length than in the case of the universal conductance fluctuations in the
metallic regime, where
. This is a weaker dependence on
the
wire length than in the case of the universal conductance fluctuations in the
metallic regime, where 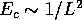 (Lee and Stone 1985)). It should also be noted
that the conductance falls faster near the band center than elsewhere (this
will be clear from
the results for the average conductance). When the system is in the strong
localization regime, the conductance is reduced to a set of peaks
of different amplitudes, with maximum value of
(Lee and Stone 1985)). It should also be noted
that the conductance falls faster near the band center than elsewhere (this
will be clear from
the results for the average conductance). When the system is in the strong
localization regime, the conductance is reduced to a set of peaks
of different amplitudes, with maximum value of 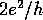 (see Fig. 2
(see Fig. 2
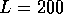 ). The mechanism of electron transport is resonant tunnelling through
the quantum wire (Bryant 1991). When the energy of an electron coincides with
an eigenenergy of the wire the electron can be transmitted through the wire via
this localized state. The height of the peak of
). The mechanism of electron transport is resonant tunnelling through
the quantum wire (Bryant 1991). When the energy of an electron coincides with
an eigenenergy of the wire the electron can be transmitted through the wire via
this localized state. The height of the peak of 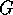 depends on the overlap
between the wavefunctions of this spatially
localized state inside the wire and the propagating states in the leads. As the
length of the wire is further increased, the number of peaks and their
amplitudes reduce and their positions change. The highest such peaks are
probably due to tunnelling through multiple resonant states, so-called
`necklace' states (Pendry 1987).
depends on the overlap
between the wavefunctions of this spatially
localized state inside the wire and the propagating states in the leads. As the
length of the wire is further increased, the number of peaks and their
amplitudes reduce and their positions change. The highest such peaks are
probably due to tunnelling through multiple resonant states, so-called
`necklace' states (Pendry 1987).
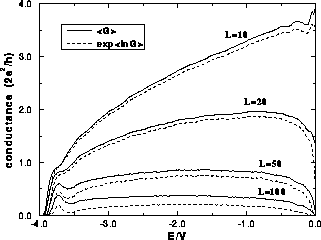
Figure 3: Average conductance as a function of energy, for quantum wires with
rough boundary and no island disorder, for different wire lengths:
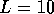 ,
, 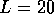 ,
, 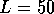 and
and 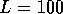 . Number of samples
taken for calculating average values are:
. Number of samples
taken for calculating average values are: 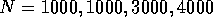 for wire lengths
for wire lengths 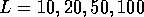 respectively.
respectively.
Next we discuss the results for the ensemble average conductance and for the
conductance fluctuations. Fig. 3 shows results for 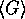 and
and 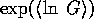 . Conductance quantization disappears
very quickly, although the presence of a short plateau for the first
subband can be observed for the shorter wires. The boundary roughness has less
impact for longer wavelengths (smaller energies) and hence the average
conductance tends to decrease with increasing energy. As the length of the
wire increases there is a rapid decrease of
. Conductance quantization disappears
very quickly, although the presence of a short plateau for the first
subband can be observed for the shorter wires. The boundary roughness has less
impact for longer wavelengths (smaller energies) and hence the average
conductance tends to decrease with increasing energy. As the length of the
wire increases there is a rapid decrease of 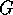 near the band center. In the
strong localization regime, a broad peak
emerges near the band edge (see Fig. 3 for
near the band center. In the
strong localization regime, a broad peak
emerges near the band edge (see Fig. 3 for  ), which
corresponds to the peak in the localization length(Nikolic and MacKinnon 1993). In this
regime, the average conductance of quasi-1D systems falls off exponentially
with the length (johnstone and Kunz 1983):
), which
corresponds to the peak in the localization length(Nikolic and MacKinnon 1993). In this
regime, the average conductance of quasi-1D systems falls off exponentially
with the length (johnstone and Kunz 1983):

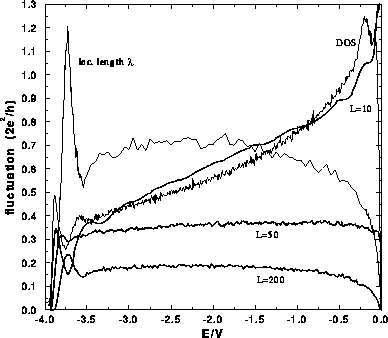
Figure 4: Conductance fluctuations which correspond to the case in
Fig. 4 for the wire lengths: 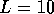 ,
, 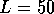 and
and 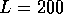 (three bold lines). Two thin lines are the localization length and the
density of states (both rescaled:
(three bold lines). Two thin lines are the localization length and the
density of states (both rescaled: 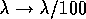 and
and
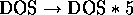 ) for quantum wires with boundary
roughness.
) for quantum wires with boundary
roughness.
The conductance fluctuations for the case of the quantum wire with boundary
roughness only, calculated for the examples from Fig. 3 by
using definition Eq. (16), are presented in
Fig. 4. Three characteristic regimes are shown:
- the quasi-ballistic regime - the wire length is comparable with the
mean free path length,
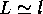 (e.g.
(e.g. 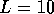 for most of the energies and
for the level of disorder assumed in our samples);
for most of the energies and
for the level of disorder assumed in our samples);
- the mesoscopic regime where the wire length is
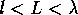 (e.g.
(e.g.
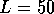 );
);
- the strong localization regime -
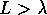 (e.g.
(e.g. 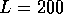 ).
).
Since the elastic mean free path and the localization length are both functions
of energy, a particular wire can move between these regimes as the energy is
changed. The fluctuations for the case 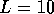 in Fig. 4 show
interesting similarities with the density of states for the same type of
quantum wires. There is a peak near the band edge which corresponds to the peak
in the DOS, which is the last remaining feature of the inverse square root
singularities from the DOS of clean quasi-1D systems (see Nikolic and MacKinnon 1993). This behaviour can be explained in the following way.
For short wires (i.e. quasi-ballistic transport) the important length is the
elastic mean free path
in Fig. 4 show
interesting similarities with the density of states for the same type of
quantum wires. There is a peak near the band edge which corresponds to the peak
in the DOS, which is the last remaining feature of the inverse square root
singularities from the DOS of clean quasi-1D systems (see Nikolic and MacKinnon 1993). This behaviour can be explained in the following way.
For short wires (i.e. quasi-ballistic transport) the important length is the
elastic mean free path 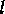 . If
. If 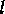 increases (as a function of energy) in the
quasi-ballistic regime, then the conductance fluctuations decrease - as the
scattering in the wire is reduced, and vice versa. Since
increases (as a function of energy) in the
quasi-ballistic regime, then the conductance fluctuations decrease - as the
scattering in the wire is reduced, and vice versa. Since 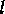 is roughly
inversely proportional to the DOS (when the DOS is increased the scattering
rate increases and therefore
is roughly
inversely proportional to the DOS (when the DOS is increased the scattering
rate increases and therefore 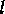 decreases), then the conductance fluctuations
might be expected to mirror the DOS. As
decreases), then the conductance fluctuations
might be expected to mirror the DOS. As 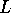 is increased with respect to
is increased with respect to 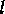 (and still
(and still 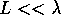 ) then the fluctuations will increase towards their
maximal value, which is reached in the mesoscopic regime. The quantum wires of
length
) then the fluctuations will increase towards their
maximal value, which is reached in the mesoscopic regime. The quantum wires of
length 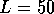 in Fig. 4 show a relatively wide region of energy in
which the conductance fluctuations are independent of energy, with a value
which is close to the universal value for quasi-1D systems (
in Fig. 4 show a relatively wide region of energy in
which the conductance fluctuations are independent of energy, with a value
which is close to the universal value for quasi-1D systems (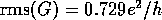 (Lee and Stone 1985)).
(Lee and Stone 1985)).
For long wires (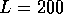 ) we have the strong localization regime and
) we have the strong localization regime and 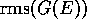 follows the curve for the localization length
follows the curve for the localization length 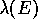 (see
Fig. 4), i.e. the average conductance, since these are related
(Eq. 17). That
(see
Fig. 4), i.e. the average conductance, since these are related
(Eq. 17). That 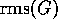 and
and 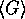 are proportional can be
understood by using the picture of `open' and `shut' channels, or `maximal
fluctuations', in a quantum wire in the strong localization regime
(Pendry et al. 1992).
This terminology is associated with the distribution function
are proportional can be
understood by using the picture of `open' and `shut' channels, or `maximal
fluctuations', in a quantum wire in the strong localization regime
(Pendry et al. 1992).
This terminology is associated with the distribution function 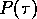 for the
eigenvalues
for the
eigenvalues  (
( ) of
) of 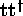 , where
, where  is the transmission matrix: it has a peak at
is the transmission matrix: it has a peak at 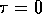 , and a tail which
extends to
, and a tail which
extends to 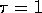 (Pendry et al. 1992, MacKinnon 1992). Each eigenvector of
(Pendry et al. 1992, MacKinnon 1992). Each eigenvector of 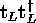 defines a conducting `micro-channel' with the
corresponding conductance
defines a conducting `micro-channel' with the
corresponding conductance  in units of
in units of 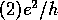 (Pendry et al. 1992). As
the size of the system is increased, the peak at
(Pendry et al. 1992). As
the size of the system is increased, the peak at 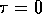 strengthens at the
expense of the tail, but the shape of the tail remains the same.
strengthens at the
expense of the tail, but the shape of the tail remains the same.
For long lengths, therefore, most of the micro-channels will have conductance
of order 0 since the bulk of the distribution is around 0. Only a small
fraction of the channels, with values for  of order 1 (roughly
of order 1 (roughly
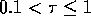 ), will contribute to the conductance. Such a distribution of
), will contribute to the conductance. Such a distribution of
 , implies that the fluctuations tend to the maximum possible value
consistent with their mean. However, the moments of the conductance,
, implies that the fluctuations tend to the maximum possible value
consistent with their mean. However, the moments of the conductance,
 , for 2D and 3D cases do not show
the same size dependence as the moments of
, for 2D and 3D cases do not show
the same size dependence as the moments of 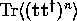 , within the metallic regime. Universal conductance
fluctuations are affected by the correlations between the
, within the metallic regime. Universal conductance
fluctuations are affected by the correlations between the  s rather than
by the distribution of the
s rather than
by the distribution of the  s themselves. UCFs (i.e. with a universal value
ca.
s themselves. UCFs (i.e. with a universal value
ca. 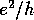 ) are restricted to disordered systems in the metallic regime where
perturbation theory is applicable. When localization effects are important,
however, the correlations between the micro-channels change and a different
sort of fluctuations is observed (Pendry et al. 1992). The statistics of a single
micro-channel were found to be crucial in the strong localization regime.
) are restricted to disordered systems in the metallic regime where
perturbation theory is applicable. When localization effects are important,
however, the correlations between the micro-channels change and a different
sort of fluctuations is observed (Pendry et al. 1992). The statistics of a single
micro-channel were found to be crucial in the strong localization regime.
The average conductance of the disordered quasi-1D system shows an
asymptotically
exponential decrease with the length (johnstone and Kunz 1983). This single parameter
dependence suggests that the conductance statistics of quasi-1D samples, with
a length much longer than the localization length, is dominated by a single
channel. Hence a similar size dependence for the conductance moments should be
expected as for 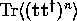 , since
the distribution of
, since
the distribution of  s is important, rather than the correlation between
them. This picture of the conductance statistics in the strong localization
regime shows that the conductance fluctuations are proportional to the average
conductance.
s is important, rather than the correlation between
them. This picture of the conductance statistics in the strong localization
regime shows that the conductance fluctuations are proportional to the average
conductance.
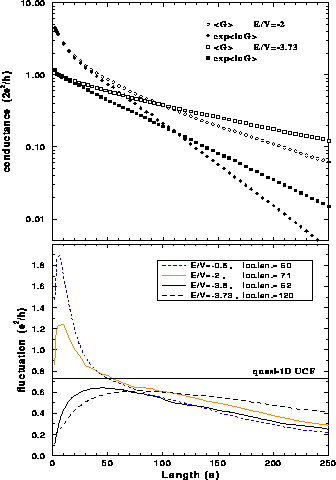
Figure 5: Average conductance as a function of wire length for real wire
without islands for energies 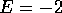 and
and 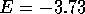 - top figure.
The corresponding conductance fluctuations are
shown in the lower figure as well as fluctuations for energies
- top figure.
The corresponding conductance fluctuations are
shown in the lower figure as well as fluctuations for energies 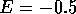 and
and 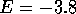 . Number of samples is
. Number of samples is 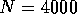 .
.
In Fig. 5 results are given for the conductance as a function
of wire length, for a fixed energy. The results for the average conductance
are presented for two values of the energy and two more examples of conductance
fluctuations are added. The decrease of conductance is more marked in the
quasi-ballistic (near ballistic) regime (short wires), where the difference
between  and
and 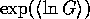 is negligible.
The difference between the two averages increases as the disorder or length of
the wire is increased (Figures 3 and 5). This
shows that the average
is negligible.
The difference between the two averages increases as the disorder or length of
the wire is increased (Figures 3 and 5). This
shows that the average 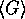 is dominated by a small number of
samples with conductance of order
is dominated by a small number of
samples with conductance of order 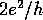 . The divergence of the two curves
indicates that the conductance distribution is transforming to the form which
has a peak for small conductances and a long tail towards larger conductances,
i.e. it is transforming to a log-normal distribution (johnstone and Kunz 1983).
For wires of length
. The divergence of the two curves
indicates that the conductance distribution is transforming to the form which
has a peak for small conductances and a long tail towards larger conductances,
i.e. it is transforming to a log-normal distribution (johnstone and Kunz 1983).
For wires of length 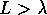 the decrease of the average conductance
the decrease of the average conductance
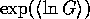 with the length of the wire is mainly determined by
the localization length. The value for the localization length can be obtained
from Fig. 5, where
with the length of the wire is mainly determined by
the localization length. The value for the localization length can be obtained
from Fig. 5, where 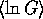 is fitted with a
straight line and
is fitted with a
straight line and 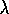 is determined from its slope,
is determined from its slope,

for wires of length 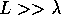 .
.
The results for the conductance fluctuations are also shown in
Fig. 5. The fluctuations first increase for very short wire
lengths (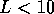 ). This is the nearly ballistic regime where the fluctuations
grow as the disorder (or wire length) increases. On the other side, for long
wires, i.e. the strong localization regime (
). This is the nearly ballistic regime where the fluctuations
grow as the disorder (or wire length) increases. On the other side, for long
wires, i.e. the strong localization regime (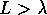 ), the fluctuations
decrease as the wire
becomes longer, due to the overall decrease of the conductance. In this regime
the fluctuations between wires of the same length depend only on the
localization length (see Fig. 5). The fluctuations take
maximal values between these two regimes.
Fluctuations for wires with many subbands (
), the fluctuations
decrease as the wire
becomes longer, due to the overall decrease of the conductance. In this regime
the fluctuations between wires of the same length depend only on the
localization length (see Fig. 5). The fluctuations take
maximal values between these two regimes.
Fluctuations for wires with many subbands (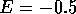 and
and 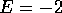 in
Fig. 5) have a sharp peak for short lengths and then start to
decrease well before the wire has become longer than
in
Fig. 5) have a sharp peak for short lengths and then start to
decrease well before the wire has become longer than 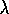 . The
fluctuations in the wires with a few subbands (
. The
fluctuations in the wires with a few subbands (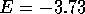 and
and 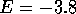 Fig. 5) even appear to be independent of length for several
ranges of
Fig. 5) even appear to be independent of length for several
ranges of 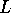 in the intermediate region. This could be called the universal
region (Ando and Tamura 1992, Tamura and Ando 1991), although the constant value of the conductance
fluctuations is not equal to the universal value
obtained for quasi-1D systems in the perturbation theory (Lee and Stone 1985).
in the intermediate region. This could be called the universal
region (Ando and Tamura 1992, Tamura and Ando 1991), although the constant value of the conductance
fluctuations is not equal to the universal value
obtained for quasi-1D systems in the perturbation theory (Lee and Stone 1985).



Next: The Influence of
Up: Conductance and conductance fluctuations
Previous: Model and Methods
Angus MacKinnon
Fri Nov 18 13:59:27 gmt 1994

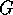 as a function of energy of a single sample of quantum wire
with rough edges and no island disorder, for wire lengths:
as a function of energy of a single sample of quantum wire
with rough edges and no island disorder, for wire lengths: 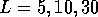 and
and 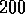 , and average wire width
, and average wire width 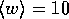 and leads width
and leads width 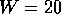 .
Reference step functions are the conductances of the perfect wire of the
width
.
Reference step functions are the conductances of the perfect wire of the
width 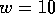 , length
, length 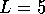 , and leads with
, and leads with 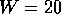 (full line), and
(full line), and 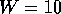 (i.e. no difference between leads and wire - broken line). The
inset is the conductance of a quantum wire
sample as a function of the wire length. The top picture shows the
geometry of the lead-wire-lead system used in the calculations.
(i.e. no difference between leads and wire - broken line). The
inset is the conductance of a quantum wire
sample as a function of the wire length. The top picture shows the
geometry of the lead-wire-lead system used in the calculations.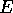 and wire length
and wire length 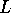 .
Firstly, we discuss the results for the conductance of a single quantum wire
sample, presented in Fig. 2.
.
Firstly, we discuss the results for the conductance of a single quantum wire
sample, presented in Fig. 2.
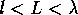 , the conductance
curve shows sample specific fluctuations as a function of energy and length.
However, the
amplitude of these fluctuations is of order
, the conductance
curve shows sample specific fluctuations as a function of energy and length.
However, the
amplitude of these fluctuations is of order 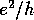 , independent of energy
(Fig.
, independent of energy
(Fig. 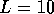 and
and 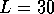 ) or with
the level of disorder. This observation supports the idea that the
fluctuations do not arise from classical scattering from the rough boundary
but from the phase modulation of the electron wavefunction due to multiple
elastic
scattering in the wire (
) or with
the level of disorder. This observation supports the idea that the
fluctuations do not arise from classical scattering from the rough boundary
but from the phase modulation of the electron wavefunction due to multiple
elastic
scattering in the wire (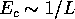 . This is a weaker dependence on
the
wire length than in the case of the universal conductance fluctuations in the
metallic regime, where
. This is a weaker dependence on
the
wire length than in the case of the universal conductance fluctuations in the
metallic regime, where 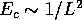 (
(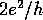 (see Fig.
(see Fig. 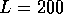 ). The mechanism of electron transport is resonant tunnelling through
the quantum wire (
). The mechanism of electron transport is resonant tunnelling through
the quantum wire (
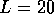 ,
, 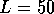 and
and 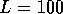 . Number of samples
taken for calculating average values are:
. Number of samples
taken for calculating average values are: 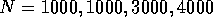 for wire lengths
for wire lengths 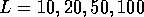 respectively.
respectively.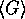 and
and 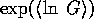 . Conductance quantization disappears
very quickly, although the presence of a short plateau for the first
subband can be observed for the shorter wires. The boundary roughness has less
impact for longer wavelengths (smaller energies) and hence the average
conductance tends to decrease with increasing energy. As the length of the
wire increases there is a rapid decrease of
. Conductance quantization disappears
very quickly, although the presence of a short plateau for the first
subband can be observed for the shorter wires. The boundary roughness has less
impact for longer wavelengths (smaller energies) and hence the average
conductance tends to decrease with increasing energy. As the length of the
wire increases there is a rapid decrease of 

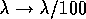 and
and
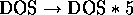 ) for quantum wires with boundary
roughness.
) for quantum wires with boundary
roughness.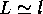 (e.g.
(e.g. 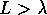 (e.g.
(e.g. 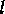 . If
. If 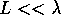 ) then the fluctuations will increase towards their
maximal value, which is reached in the mesoscopic regime. The quantum wires of
length
) then the fluctuations will increase towards their
maximal value, which is reached in the mesoscopic regime. The quantum wires of
length 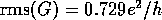 (Lee and Stone 1985)).
(Lee and Stone 1985)).
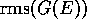 follows the curve for the localization length
follows the curve for the localization length 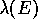 (see
Fig.
(see
Fig. 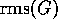 and
and 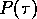 for the
eigenvalues
for the
eigenvalues  (
( ) of
) of 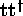 , where
, where  is the transmission matrix: it has a peak at
is the transmission matrix: it has a peak at 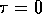 , and a tail which
extends to
, and a tail which
extends to 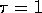 (
(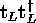 defines a conducting `micro-channel' with the
corresponding conductance
defines a conducting `micro-channel' with the
corresponding conductance 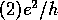 (
(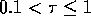 ), will contribute to the conductance. Such a distribution of
), will contribute to the conductance. Such a distribution of
 , for 2D and 3D cases do not show
the same size dependence as the moments of
, for 2D and 3D cases do not show
the same size dependence as the moments of 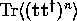 , within the metallic regime. Universal conductance
fluctuations are affected by the correlations between the
, within the metallic regime. Universal conductance
fluctuations are affected by the correlations between the 
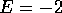 and
and 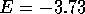 - top figure.
The corresponding conductance fluctuations are
shown in the lower figure as well as fluctuations for energies
- top figure.
The corresponding conductance fluctuations are
shown in the lower figure as well as fluctuations for energies 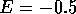 and
and 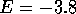 . Number of samples is
. Number of samples is 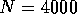 .
.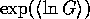 is negligible.
The difference between the two averages increases as the disorder or length of
the wire is increased (Figures
is negligible.
The difference between the two averages increases as the disorder or length of
the wire is increased (Figures 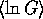 is fitted with a
straight line and
is fitted with a
straight line and 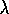 is determined from its slope,
is determined from its slope,

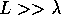 .
.
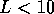 ). This is the nearly ballistic regime where the fluctuations
grow as the disorder (or wire length) increases. On the other side, for long
wires, i.e. the strong localization regime (
). This is the nearly ballistic regime where the fluctuations
grow as the disorder (or wire length) increases. On the other side, for long
wires, i.e. the strong localization regime (