INTRODUCTION



Next: Model and Methods
Up: Conductance and conductance fluctuations
Previous: Conductance and conductance fluctuations
Many novel transport phenomena have been revealed in mesoscopic
low-dimensional structures. The considerable interest in submicron
electronic structures has been motivated by the expectation that
potentially useful new devices could be invented. Very sophisticated
techniques have been developed, such as the various types of epitaxial
growth, lithography, ion implantation, etching and cleaving,
etc. in order to make these small size structures. However,
none of them can produce perfect quantum wires. For example, GaAs/AlAs
quantum well wires grown on a vicinal surface using molecular-beam
epitaxy (MBE) (Petroff et al. 1984) have two characteristic types of
disorder. The interface between the GaAs and the AlAs regions is not
smooth and, in addition, within the region of nominally pure GaAs,
there will be islands of AlAs. The question of how compositional
disorder affects the transport properties of quantum wires is
important.
The conductance of narrow ballistic channels, or quantum point
contacts in a 2D electron gas (2DEG) is quantized in integer multiples
of 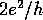 (van Wees et al. 1988, Wharam et al. 1988).
However, this simple step-like form for the conductance as a function
of the Fermi energy, occurs when the transition between the wide leads
and the narrow channel is adiabatic(Glazman et al. 1988, Glazman and Jonson 1990). Nonadiabatic, i.e.
mode-mixing transport through the constriction produces some additional
features in the conductance diagram
(Kirczenow et al. 1988, Szafer and Stone 1989, Song and Das Sarma 1993, Nikolic 1983). The conditions for adiabatic
transport are readily achieved in the experiments. Disorder, however, can
quite easily destroy conductance quantization. Poor quantization is
believed to be mainly caused by backscattering. Backscattering, at low
temperatures, is produced by the impurities within the wire and/or by
the rough wire edge. It can also be caused indirectly through resonant
states trapped in the wire, which may be created by the random field of
impurities outside the wire (Nixon et al. 1991, Laughton et al. 1991). However,
forward scattering does not generally harm the conductance
quantization, if all conducting modes are fully occupied
(Laughton et al. 1991). Small-angle backscattering predominates in the
highest subbands and is usually considered responsible for the
destruction of the conductance quantization. When only the lowest 1D
subband is occupied, however, the number of states into which an
electron can be scattered by disorder is reduced. This gave rise to the
prediction of a large electron mobility in a confined electron system
(Sakaki 1980). However, the conductance is very strongly influenced
by the quantum interference effects which start to emerge as elastic
scattering is intrrough boundariesoduced in the ballistic regime. In the quasi-1D
case there is a much higher probability of multiple scattering from the
same site compared to the 2D or 3D case. This could cause Anderson
localization to become dominant.
(van Wees et al. 1988, Wharam et al. 1988).
However, this simple step-like form for the conductance as a function
of the Fermi energy, occurs when the transition between the wide leads
and the narrow channel is adiabatic(Glazman et al. 1988, Glazman and Jonson 1990). Nonadiabatic, i.e.
mode-mixing transport through the constriction produces some additional
features in the conductance diagram
(Kirczenow et al. 1988, Szafer and Stone 1989, Song and Das Sarma 1993, Nikolic 1983). The conditions for adiabatic
transport are readily achieved in the experiments. Disorder, however, can
quite easily destroy conductance quantization. Poor quantization is
believed to be mainly caused by backscattering. Backscattering, at low
temperatures, is produced by the impurities within the wire and/or by
the rough wire edge. It can also be caused indirectly through resonant
states trapped in the wire, which may be created by the random field of
impurities outside the wire (Nixon et al. 1991, Laughton et al. 1991). However,
forward scattering does not generally harm the conductance
quantization, if all conducting modes are fully occupied
(Laughton et al. 1991). Small-angle backscattering predominates in the
highest subbands and is usually considered responsible for the
destruction of the conductance quantization. When only the lowest 1D
subband is occupied, however, the number of states into which an
electron can be scattered by disorder is reduced. This gave rise to the
prediction of a large electron mobility in a confined electron system
(Sakaki 1980). However, the conductance is very strongly influenced
by the quantum interference effects which start to emerge as elastic
scattering is intrrough boundariesoduced in the ballistic regime. In the quasi-1D
case there is a much higher probability of multiple scattering from the
same site compared to the 2D or 3D case. This could cause Anderson
localization to become dominant.
The conductance fluctuations are expected to show peculiar behaviour in
narrow quantum wires (Tamura and Ando 1991, Ando and Tamura 1992). In the metallic regime all
the dimensions of a sample are much larger than the mean free path 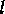 and
the electron motion is well defined in all directions. Hence, the
perturbation theory approach based on Feynman diagrams, which yields
universal conductance fluctuations (UCF), is valid. However, the
transverse quantization in quantum wires gives well resolved 1D
subbands if the width of the wire (
and
the electron motion is well defined in all directions. Hence, the
perturbation theory approach based on Feynman diagrams, which yields
universal conductance fluctuations (UCF), is valid. However, the
transverse quantization in quantum wires gives well resolved 1D
subbands if the width of the wire (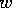 ) is smaller than the mean free
path (
) is smaller than the mean free
path (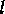 ) and comparable to the Fermi wavelength
) and comparable to the Fermi wavelength 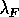 .
Therefore, in general, UCFs are not expected in quantum wires with weak
disorder. On the other hand we know that in the case of strong disorder
when the wire length
.
Therefore, in general, UCFs are not expected in quantum wires with weak
disorder. On the other hand we know that in the case of strong disorder
when the wire length 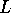 becomes greater than the localization length
becomes greater than the localization length
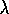 , subband mixing is very strong and any quasi-1D feature of a
perfect system is virtually destroyed (Taylor et al. 1991, Nikolic and MacKinnon 1993). Then
it becomes essential to take localization effects into account.
Again, application of a perturbational method (Stone 1992)) is
inappropriate.
, subband mixing is very strong and any quasi-1D feature of a
perfect system is virtually destroyed (Taylor et al. 1991, Nikolic and MacKinnon 1993). Then
it becomes essential to take localization effects into account.
Again, application of a perturbational method (Stone 1992)) is
inappropriate.
Here we examine the influence of
rough boundaries,
impurities,
and both types of disorder
combined
on the conductance and conductance
fluctuations of quantum wires at zero temperature and zero magnetic
field. All calculations were done using a Landauer-type formula for
the conductance.



Next: Model and Methods
Up: Conductance and conductance fluctuations
Previous: Conductance and conductance fluctuations
Angus MacKinnon
Fri Nov 18 13:59:27 gmt 1994
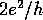 (van Wees et al. 1988, Wharam et al. 1988).
However, this simple step-like form for the conductance as a function
of the Fermi energy, occurs when the transition between the wide leads
and the narrow channel is adiabatic(Glazman et al. 1988, Glazman and Jonson 1990). Nonadiabatic, i.e.
mode-mixing transport through the constriction produces some additional
features in the conductance diagram
(Kirczenow et al. 1988, Szafer and Stone 1989, Song and Das Sarma 1993, Nikolic 1983). The conditions for adiabatic
transport are readily achieved in the experiments. Disorder, however, can
quite easily destroy conductance quantization. Poor quantization is
believed to be mainly caused by backscattering. Backscattering, at low
temperatures, is produced by the impurities within the wire and/or by
the rough wire edge. It can also be caused indirectly through resonant
states trapped in the wire, which may be created by the random field of
impurities outside the wire (Nixon et al. 1991, Laughton et al. 1991). However,
forward scattering does not generally harm the conductance
quantization, if all conducting modes are fully occupied
(Laughton et al. 1991). Small-angle backscattering predominates in the
highest subbands and is usually considered responsible for the
destruction of the conductance quantization. When only the lowest 1D
subband is occupied, however, the number of states into which an
electron can be scattered by disorder is reduced. This gave rise to the
prediction of a large electron mobility in a confined electron system
(Sakaki 1980). However, the conductance is very strongly influenced
by the quantum interference effects which start to emerge as elastic
scattering is intrrough boundariesoduced in the ballistic regime. In the quasi-1D
case there is a much higher probability of multiple scattering from the
same site compared to the 2D or 3D case. This could cause Anderson
localization to become dominant.
(van Wees et al. 1988, Wharam et al. 1988).
However, this simple step-like form for the conductance as a function
of the Fermi energy, occurs when the transition between the wide leads
and the narrow channel is adiabatic(Glazman et al. 1988, Glazman and Jonson 1990). Nonadiabatic, i.e.
mode-mixing transport through the constriction produces some additional
features in the conductance diagram
(Kirczenow et al. 1988, Szafer and Stone 1989, Song and Das Sarma 1993, Nikolic 1983). The conditions for adiabatic
transport are readily achieved in the experiments. Disorder, however, can
quite easily destroy conductance quantization. Poor quantization is
believed to be mainly caused by backscattering. Backscattering, at low
temperatures, is produced by the impurities within the wire and/or by
the rough wire edge. It can also be caused indirectly through resonant
states trapped in the wire, which may be created by the random field of
impurities outside the wire (Nixon et al. 1991, Laughton et al. 1991). However,
forward scattering does not generally harm the conductance
quantization, if all conducting modes are fully occupied
(Laughton et al. 1991). Small-angle backscattering predominates in the
highest subbands and is usually considered responsible for the
destruction of the conductance quantization. When only the lowest 1D
subband is occupied, however, the number of states into which an
electron can be scattered by disorder is reduced. This gave rise to the
prediction of a large electron mobility in a confined electron system
(Sakaki 1980). However, the conductance is very strongly influenced
by the quantum interference effects which start to emerge as elastic
scattering is intrrough boundariesoduced in the ballistic regime. In the quasi-1D
case there is a much higher probability of multiple scattering from the
same site compared to the 2D or 3D case. This could cause Anderson
localization to become dominant.
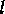 and
the electron motion is well defined in all directions. Hence, the
perturbation theory approach based on Feynman diagrams, which yields
universal conductance fluctuations (UCF), is valid. However, the
transverse quantization in quantum wires gives well resolved 1D
subbands if the width of the wire (
and
the electron motion is well defined in all directions. Hence, the
perturbation theory approach based on Feynman diagrams, which yields
universal conductance fluctuations (UCF), is valid. However, the
transverse quantization in quantum wires gives well resolved 1D
subbands if the width of the wire (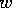 ) is smaller than the mean free
path (
) is smaller than the mean free
path (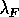 .
Therefore, in general, UCFs are not expected in quantum wires with weak
disorder. On the other hand we know that in the case of strong disorder
when the wire length
.
Therefore, in general, UCFs are not expected in quantum wires with weak
disorder. On the other hand we know that in the case of strong disorder
when the wire length 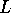 becomes greater than the localization length
becomes greater than the localization length
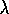 , subband mixing is very strong and any quasi-1D feature of a
perfect system is virtually destroyed (
, subband mixing is very strong and any quasi-1D feature of a
perfect system is virtually destroyed (